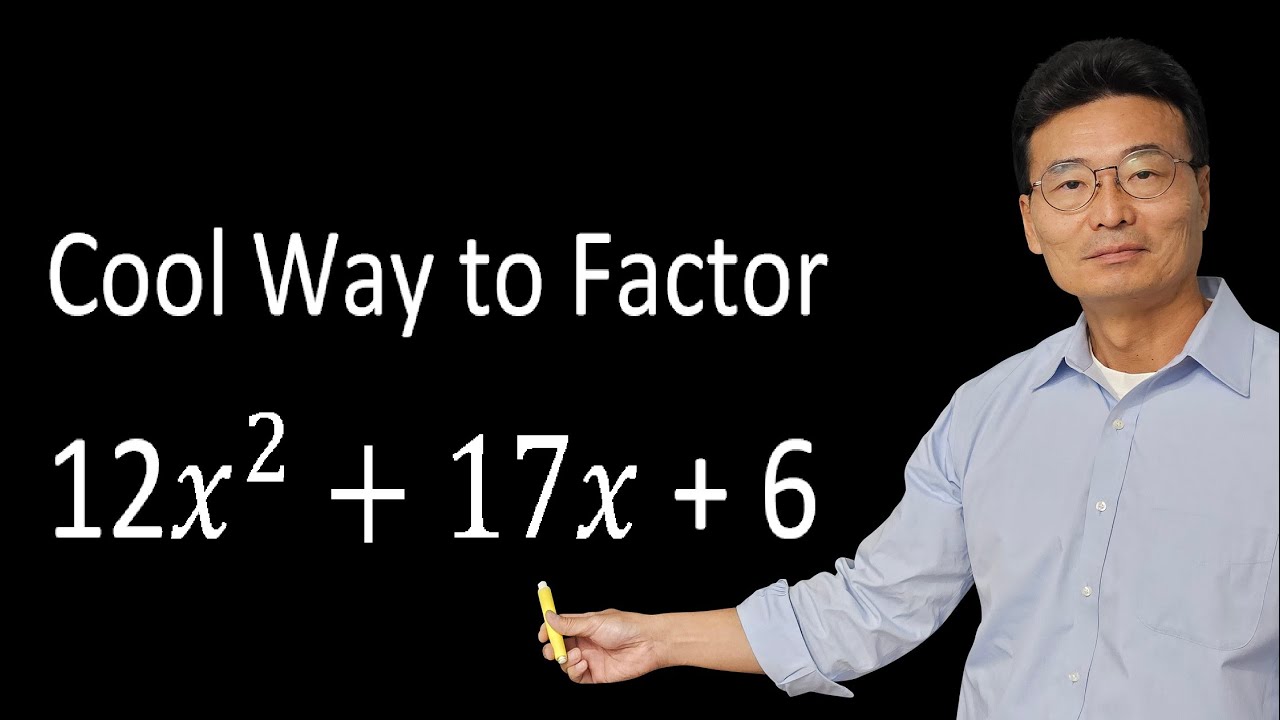Factoring Trinomials using the AC Method

Summary

This lesson delves into the AC method for factoring trinomials, which becomes more complex when the coefficient 'a' isn't 1. The instructor guides through the process of identifying coefficients 'a', 'b', and 'c', and finding two numbers whose product is 'a*c' and sum is 'b'. The method involves expanding the middle term using these numbers and then factoring by grouping. The video covers examples with single and multiple variables, demonstrating that the presence of a second variable doesn't alter the fundamental approach. The instructor emphasizes the importance of patience and thoroughness when dealing with larger numbers that require more time to factor.

Takeaways

• 📚 The lesson focuses on factoring trinomials using the AC method, which is also known as factoring by grouping.
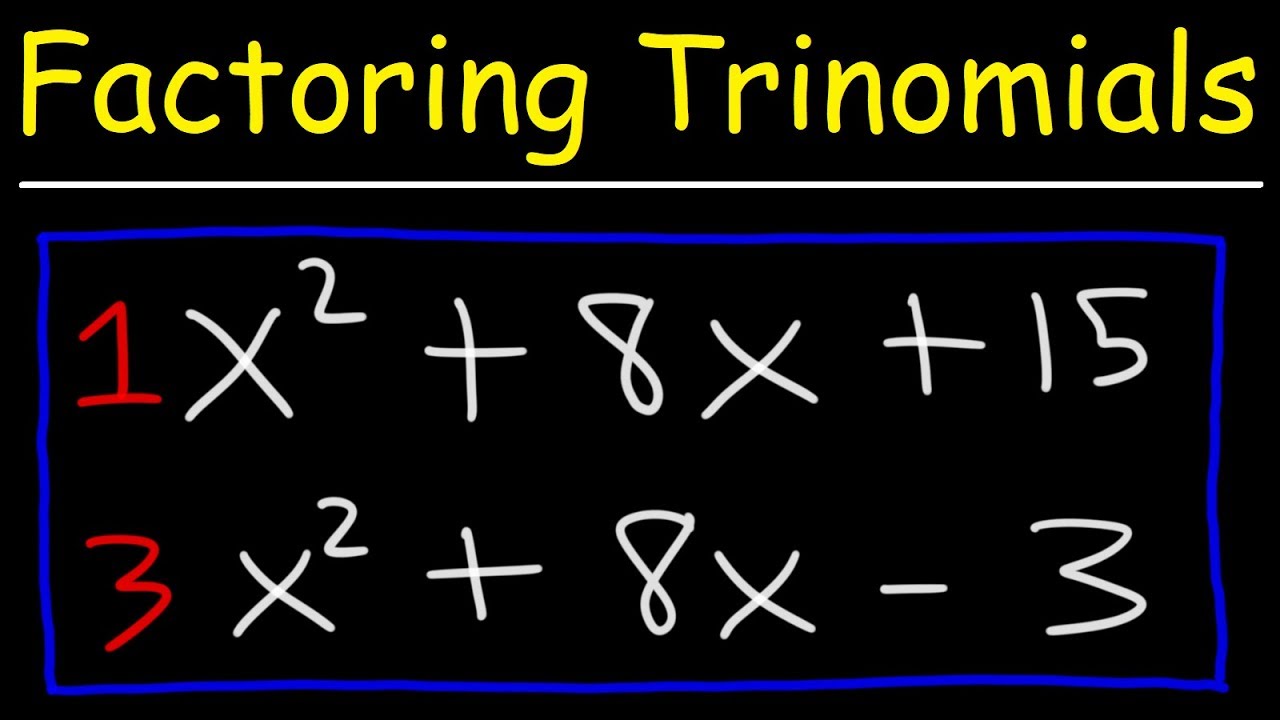
• 🔍 The simplest case scenario for factoring trinomials occurs when 'a' equals 1, allowing for straightforward factoring of the form ax^2 + bx + c.
• 🔑 To factor a trinomial, find two integers whose sum is the coefficient 'b' and whose product is the constant term 'c'.
• 🚫 If no such integers exist, the trinomial is considered prime and cannot be factored using rational numbers.
• 🤔 The AC method is more complex and involves more work, especially when 'a' is not equal to 1.
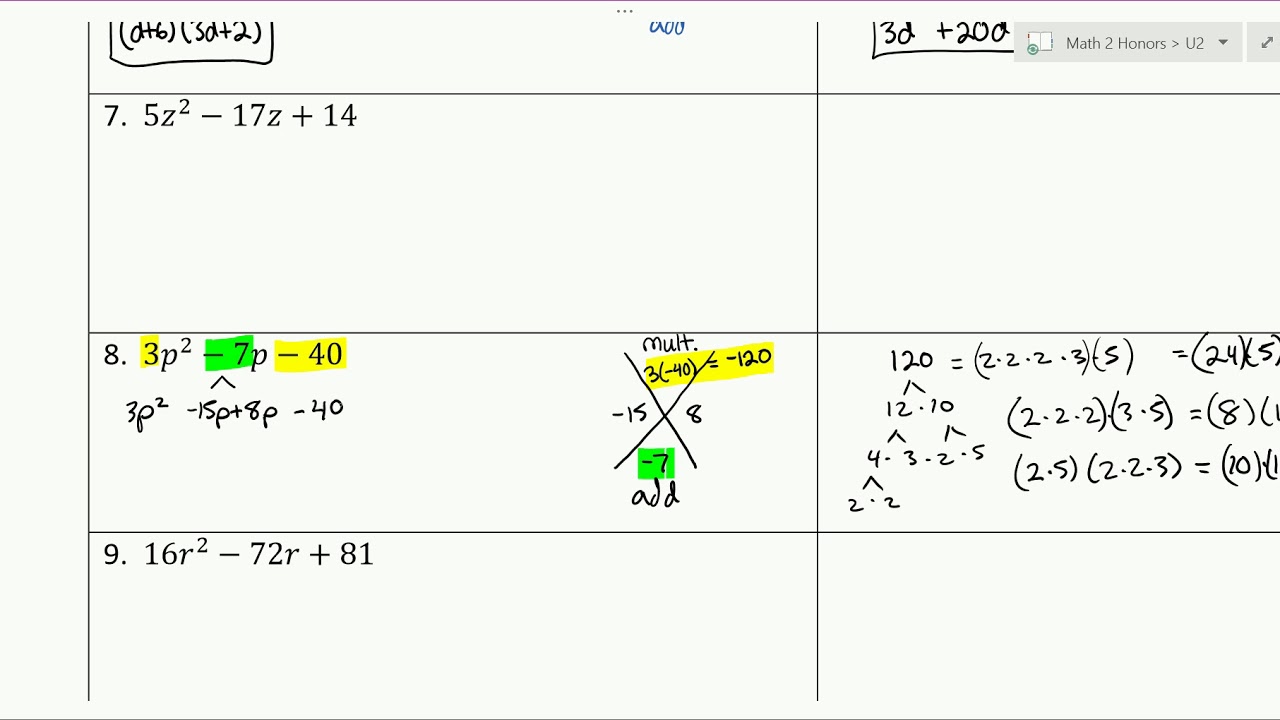
• 📈 The process involves identifying 'a', 'b', and 'c' in the trinomial and finding two integers whose product is 'a' times 'c' and whose sum is 'b'.
• 📝 The two integers found are used to expand the middle term of the trinomial, creating a four-term polynomial for further factoring.
• 🔄 The expanded polynomial is then grouped and factored by pulling out common factors from each group.
• 📉 The process can be applied to polynomials with multiple variables, as shown with the example involving 'x' and 'y'.
• 📝 The technique remains the same even with two variables, focusing on finding the correct pair of integers to expand the middle term.
• 🔍 Sometimes, the trinomial may be prime, requiring a thorough check of all factor pairs to confirm that no factorization is possible.

Q & A

What is the AC method for factoring trinomials?

The AC method, also known as the grouping method, is a technique used to factor trinomials where the coefficient 'a' is not equal to 1. It involves finding two numbers that multiply to give 'a' times 'c' (the product of the coefficient of the squared term and the constant term) and add up to 'b' (the coefficient of the linear term).

What is the simplest case scenario for factoring a trinomial?

The simplest case scenario for factoring a trinomial occurs when 'a' equals 1, which simplifies the process because the first term of each binomial is 'x', and you only need to find two integers that sum to 'b' and multiply to 'c'.

Why might a trinomial be considered prime?

A trinomial is considered prime when it cannot be factored using rational numbers. This happens when there are no two integers that satisfy both the condition of multiplying to 'a' times 'c' and adding up to 'b'.

How do you identify the coefficients 'a', 'b', and 'c' in a trinomial?

'a' is the coefficient of the squared variable, 'b' is the coefficient of the variable to the first power, and 'c' is the constant term in a trinomial of the form ax^2 + bx + c.

What is the first step in the AC method for factoring a trinomial with a not equal to 1?

The first step is to find two integers whose product is 'a' times 'c' and whose sum is 'b'. These integers help in rewriting the middle term of the trinomial to facilitate factoring by grouping.

Can the AC method be used for trinomials with two variables?

Yes, the AC method can be used for trinomials with two variables. The process remains the same, but you must consider the coefficients and variables involved, ensuring that the integers found satisfy the conditions for both variables.

What is the purpose of rewriting the middle term of the trinomial in the AC method?

Rewriting the middle term using the two integers found allows you to create a four-term polynomial that can be factored by grouping, making it easier to identify common factors and simplify the expression.

How do you check if the factorization of a trinomial is correct?

You can check the factorization by multiplying the binomial factors together and verifying that the result matches the original trinomial.

What should you do if you cannot find two integers that satisfy the conditions for the AC method?

If you cannot find two integers that satisfy the conditions, it may indicate that the trinomial is prime and cannot be factored using rational numbers.

Can the AC method be applied to trinomials with large coefficients?

Yes, the AC method can be applied to trinomials with large coefficients, but it may require more time and effort to find the correct pair of integers that meet the multiplication and addition conditions.