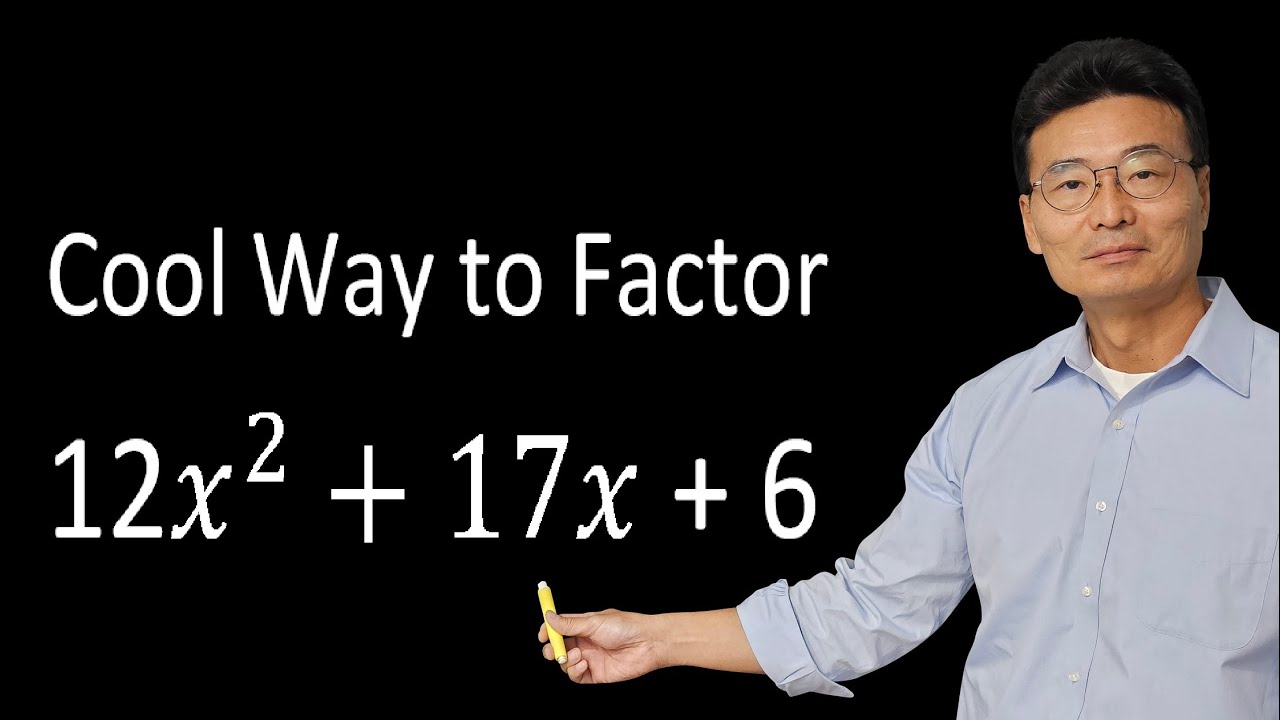Factoring Trinomials The Easy Fast Way
Summary
TLDRThis video tutorial focuses on factoring trinomials easily. It begins with simple examples where the leading coefficient is 1, teaching how to find two numbers that multiply to the constant term and add to the middle term. The process includes factoring by grouping when the leading coefficient is not 1. The tutorial also demonstrates solving quadratic equations by factoring and using the quadratic formula. Various examples are provided to illustrate each method clearly, making the video a comprehensive guide for factoring trinomials.
Takeaways
- 🔢 When factoring trinomials with a leading coefficient of 1, identify two numbers that multiply to the constant term and add to the middle term.
- ✅ Example 1: For x² + 5x + 6, the numbers 2 and 3 multiply to 6 and add to 5, so the factors are (x + 2)(x + 3).
- 📝 Example 2: For x² + 8x + 15, the numbers 3 and 5 multiply to 15 and add to 8, so the factors are (x + 3)(x + 5).
- ➖ When the middle term is negative, like in x² - 7x + 12, find numbers that multiply to the constant term and add to the negative middle term (e.g., -3 and -4 for x² - 7x + 12).
- ⚖️ For trinomials where the leading coefficient is not 1, such as 2x² - 3x - 2, multiply the first and last coefficients and find numbers that multiply to that product and add to the middle term.
- ✂️ Replace the middle term with the numbers found and factor by grouping.
- 🔍 Example: For 2x² - 3x - 2, replace -3x with -4x + x, then factor by grouping to get (2x + 1)(x - 2).
- ➕ When solving equations set equal to zero, factor the expression first, then set each factor equal to zero and solve for x.
- ⚙️ The quadratic equation can be used as an alternative method for factoring and solving quadratic equations: x = [-b ± sqrt(b² - 4ac)] / 2a.
- 🧩 Example of using the quadratic formula: For 4x² - 4x - 3, substitute into the formula and simplify to find the solutions x = 3/2 and x = -1/2.
Q & A
What is the main topic of the video?
-The main topic of the video is factoring trinomials, specifically focusing on methods to factor them easily when the leading coefficient is 1, and also when it is not 1.
What is the first trinomial example given in the video?
-The first trinomial example given in the video is x^2 + 5x + 6.
How does the video suggest finding the factors for the first trinomial example?
-The video suggests finding two numbers that multiply to 6 (the constant term) and add up to 5 (the middle term), which are 2 and 3 in this case.
What is the factored form of the first trinomial example?
-The factored form of the first trinomial example is (x + 2)(x + 3).
How can you verify the factored form of a trinomial?
-You can verify the factored form of a trinomial by using the FOIL method (First, Outer, Inner, Last) to expand the factors and check if it matches the original trinomial.
What is the process for factoring a trinomial with a leading coefficient that is not 1?
-For a trinomial with a leading coefficient that is not 1, you first multiply the leading coefficient by the constant term to find a product. Then, find two numbers that multiply to this product and add up to the middle term. Replace the middle term with these two terms and factor by grouping.
What is the second example of a trinomial given in the video?
-The second example of a trinomial given in the video is x^2 + 8x + 15.
How can you solve for x if a trinomial equals zero?
-If a trinomial equals zero, you can solve for x by setting each factor equal to zero and solving the resulting equations.
What is the quadratic equation formula mentioned in the video?
-The quadratic equation formula mentioned in the video is x = (-b ± sqrt(b^2 - 4ac)) / 2a.
Can the quadratic equation be used for all trinomials?
-Yes, the quadratic equation can be used for all trinomials, especially when factoring by grouping or other methods are difficult or not applicable.
What is the purpose of the quadratic equation in the context of the video?
-The purpose of the quadratic equation in the context of the video is to provide an alternative method for solving trinomials when factoring is not straightforward.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)