Método del trapecio | Integración numérica |Métodos Numéricos | Parte 1 | ¡Muy básico!
Summary
TLDREste vídeo explica el método del trapecio, una técnica numérica para calcular áreas bajo curvas en ingeniería. Se describe cómo seccionar un gráfico en trapecios de igual ancho (delta x) y calcular su área para aproximar la integral de una función. Se ilustra con ejemplos paso a paso, desde la división del intervalo en trapecios, el cálculo de alturas y bases, hasta la aplicación de la fórmula del área de trapecio. Se enfatiza que más trapecios resultan en una aproximación más precisa, y se compara el resultado numérico con la integración analítica para demostrar la eficacia del método.
Takeaways
- 📐 El método del trapecio es una técnica numérica para calcular áreas bajo curvas, útil en campos como la ingeniería.
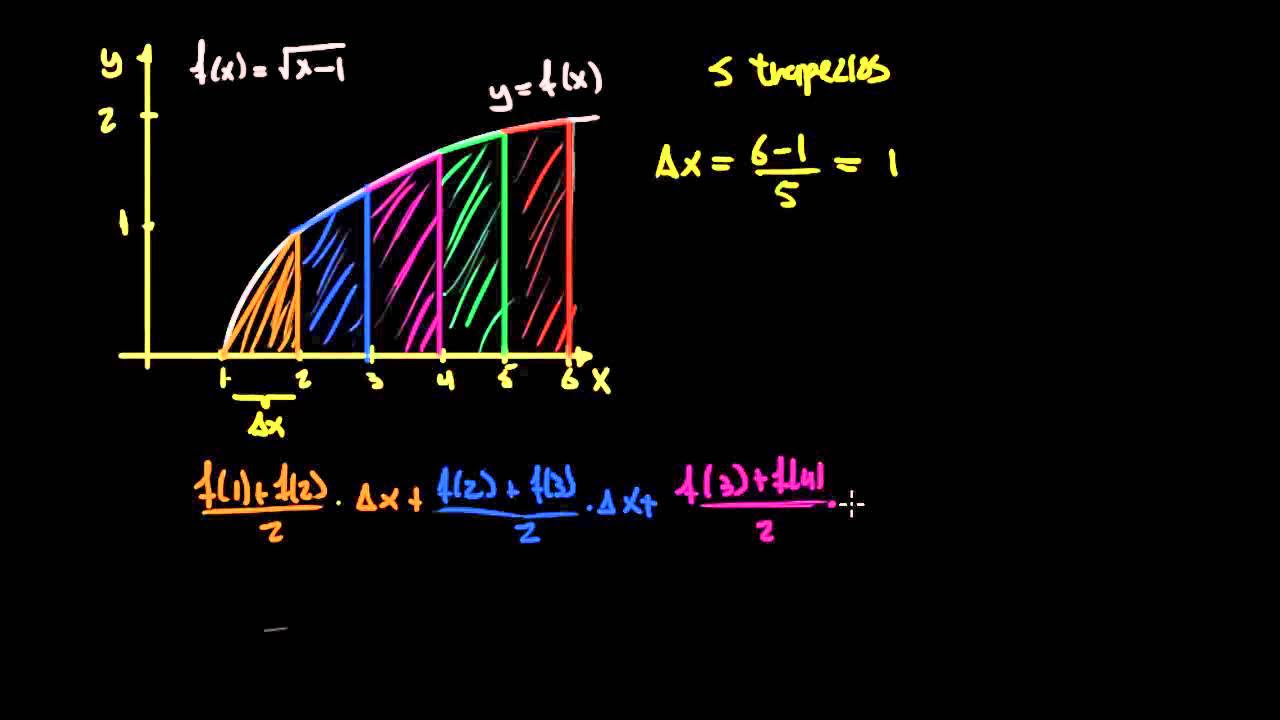
- 📈 Se divide el área bajo la curva en trapecios para aproximar la integral, siendo más preciso cuanto más pequeños sean los trapecios.
- 🔢 El cálculo del área de un trapecio se hace sumando la base mayor y la base menor, dividir entre 2 y multiplicar por la altura.
- 📉 Para mejorar la precisión, se reduce el tamaño de los intervalos (delta x) y se incrementa el número de trapecios.
- 📝 Se utiliza la fórmula delta x = (límite superior - límite inferior) / n, donde n es el número de trapecios.
- 📋 Se calcula el valor de la función en los puntos de corte para determinar las alturas de los trapecios.
- 📊 El área total se obtiene sumando el primer valor, el último valor y dos veces la suma de los valores intermedios, multiplicando todo por delta x / 2.
- 📉 El ejemplo práctico muestra cómo calcular el área bajo la curva de una función específica entre límites dados usando el método del trapecio.
- 🔍 Al comparar el resultado del método del trapecio con la integral analítica, se observa un error que disminuye con un mayor número de trapecios.
- 📊 Al aumentar el número de trapecios, como en el ejemplo de 20 o 500, se acerca más al resultado analítico, indicando mayor precisión.
Q & A
¿Qué es el método del trapecio en matemáticas?
-El método del trapecio es un método numérico utilizado para aproximar el área bajo una curva, es decir, para calcular integrales de funciones.
¿Cuál es la importancia de calcular el área bajo una curva en ingeniería?
-En ingeniería, calcular el área bajo una curva es importante para determinar magnitudes como la fuerza, el flujo de fluidos, la capacidad de almacenamiento, entre otras.
¿Cómo se determina el área de un trapecio en el método del trapecio?
-El área de un trapecio se determina mediante la fórmula: (base mayor + base menor) / 2 * altura.
¿Qué representa el delta x en el método del trapecio?
-El delta x representa el intervalo o 'espesor' de cada trapecio en la división de la curva, y es igual a (límite superior - límite inferior) / número de trapecios.
¿Cómo se calcula el área total bajo la curva utilizando el método del trapecio?
-Se suman las áreas de todos los trapecios individuales, que se calculan usando la fórmula del área de un trapecio, y se multiplica por el delta x / 2.
¿Por qué es mejor usar un mayor número de trapecios en el método del trapecio?
-Usar un mayor número de trapecios reduce el error de aproximación y aumenta la precisión del cálculo del área bajo la curva.
¿Cómo se calcula el valor de delta x cuando se usan 10 trapecios para una función definida entre 0 y 5?
-Se calcula como (5 - 0) / 10, lo que da como resultado 0.5.
¿Cuál es la fórmula general para calcular el área usando el método del trapecio?
-El área se calcula como (delta x / 2) * (f(x0) + 2 * Σ f(xi) + f(xn)), donde f(x0) es la primera altura, f(xn) es la última altura y la suma incluye las alturas de los trapecios intermedios multiplicadas por 2.
¿Cómo se evalúa la función para obtener las alturas de los trapecios?
-Se sustituyen los valores de x correspondientes a cada trapecio en la función dada para obtener las alturas f(xi).
¿Cómo se compara el resultado del método del trapecio con la integración analítica?
-Se compara el área calculada mediante el método del trapecio con el resultado de la integral analítica evaluada en los mismos límites para medir la precisión del método numérico.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)