Introducción a la integral de línea

Summary

Este video explora cómo calcular áreas bajo curvas en 2D y extiende estos conceptos a tres dimensiones, centrándose en cómo parametrizar trayectorias y calcular áreas de superficies curvas. Se analiza el uso de la integral definida para sumar áreas infinitesimales y cómo aplicar esta idea en una curva en el plano XY. También se introduce el concepto de longitud de arco y cómo se utiliza la parametrización para resolver integrales en curvas, culminando en la comprensión de la integral de línea y su relación con la longitud de la trayectoria y la función en ese punto.

Takeaways

• 😀 En el caso de dos dimensiones, el área bajo la curva se encuentra utilizando integrales definidas, que son sumas infinitas de áreas de rectángulos infinitamente estrechos.
• 😀 El área bajo la curva en 2D se calcula multiplicando el cambio infinitesimal en x (denotado como dx) por el valor de la función f(x).
• 😀 La integral definida se representa como la suma de infinitas áreas de rectángulos y permite calcular el área entre dos puntos (a y b) a lo largo del eje x.
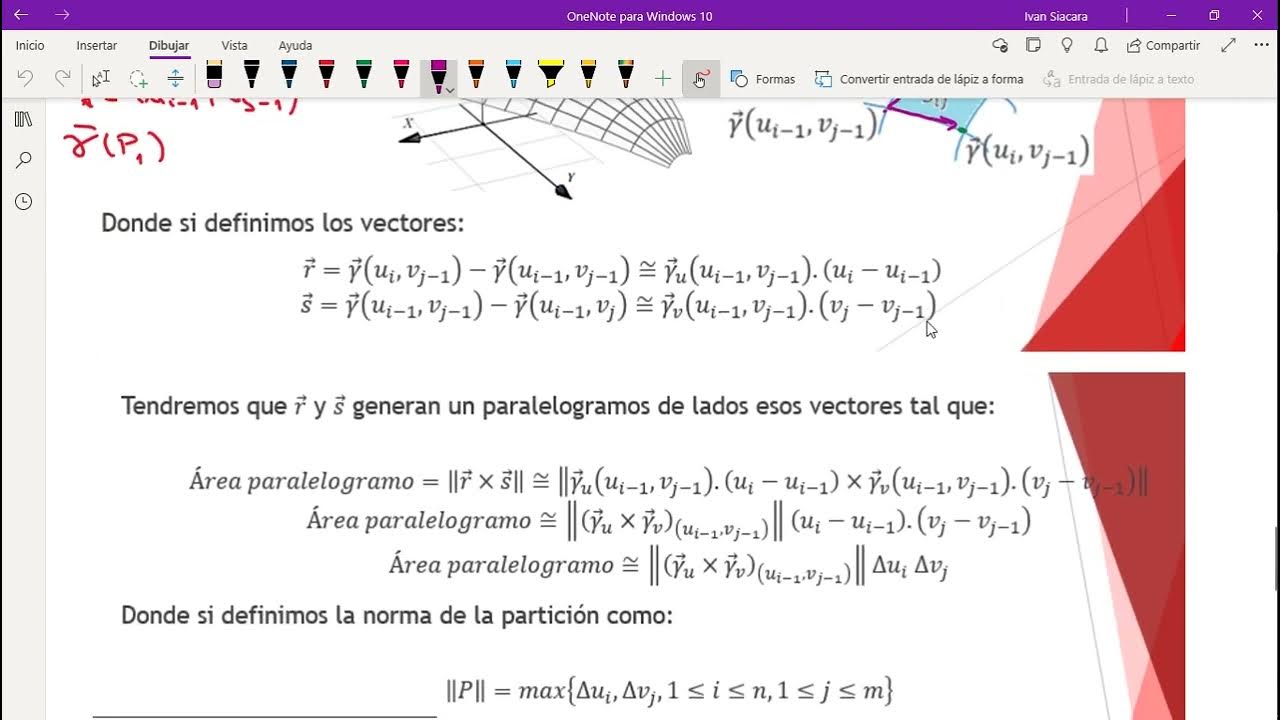
• 😀 Al extenderse a tres dimensiones, se introduce la necesidad de parametrizar las variables x y y, utilizando un parámetro t, para describir trayectorias en el plano XY.
• 😀 Un camino en el plano XY se puede describir mediante ecuaciones paramétricas para x y y, con t como el parámetro que varía entre dos valores, a y b.
• 😀 Para encontrar el área de un muro o valla curvada, se utiliza un enfoque similar al de las integrales de línea, calculando la longitud del arco y la altura de la función en cada punto.
• 😀 La longitud del arco de la curva se puede calcular utilizando el teorema de Pitágoras, sumando los cambios infinitesimales en las coordenadas x y y, para determinar el desplazamiento en la curva.
• 😀 El área bajo una curva en tres dimensiones se puede visualizar como un muro curvado a lo largo de la trayectoria de la curva, con la altura determinada por la función f(x, y).
• 😀 La integral de línea se utiliza para sumar las áreas de pequeños rectángulos que se encuentran a lo largo de una curva parametrizada, combinando los cambios en las coordenadas x y y.
• 😀 Para resolver la integral de línea, es necesario expresar todo en términos del parámetro t, lo que implica trabajar con derivadas parciales y sus respectivas longitudes de arco para calcular la integral final.

Q & A

¿Cuál es el objetivo principal de la integral definida en el contexto de este video?

El objetivo principal es calcular el área bajo una curva en dos dimensiones, utilizando la integral definida como una suma infinita de áreas de rectángulos estrechos.

¿Cómo se relaciona el concepto de área bajo una curva con la integral definida?

La integral definida se utiliza para sumar infinitamente pequeños rectángulos, donde cada rectángulo tiene un área dada por la función evaluada en un punto específico multiplicado por un pequeño cambio en x (denotado como Δx).

¿Qué ocurre cuando se extiende el problema a tres dimensiones?

Cuando se trabaja en tres dimensiones, se introduce la parametrización de las variables x y y en términos de una nueva variable t, y se asocia una función f(x, y) a cada punto en el plano xy para obtener una superficie.

¿Cómo se define un camino o trayectoria en el plano xy en este contexto?

Un camino o trayectoria en el plano xy se define mediante funciones paramétricas para x y y en términos de una variable t, con t variando entre dos valores a y b, lo que permite describir puntos a lo largo de la curva.

¿Cómo se visualiza la relación entre la función f(x, y) y la superficie en tres dimensiones?

La función f(x, y) se puede visualizar como una superficie en el espacio tridimensional, donde para cada punto en el plano xy, la función proporciona un valor en el eje vertical (eje z), formando una superficie sobre el plano.

¿Qué representa la 'cortina' mencionada en el video?

La 'cortina' se refiere a la superficie curva que se forma a lo largo de la trayectoria de la curva en el plano xy, donde la altura de cada punto de la curva está dada por el valor de la función f(x, y).

¿Qué es el cambio en la longitud de arco (ds) y cómo se relaciona con el área?

El cambio en la longitud de arco, denotado como ds, es un pequeño desplazamiento a lo largo de la curva. Al multiplicar ds por el valor de la función f(x, y) en ese punto, se obtiene el área de un pequeño rectángulo que contribuye al área total bajo la curva.

¿Cómo se calcula ds en términos de las derivadas de x y y?

El cambio en la longitud de arco ds se calcula utilizando el teorema de Pitágoras, relacionando los pequeños cambios en x y en y (denotados como dx y dy), de manera que ds es igual a la raíz cuadrada de la suma de los cuadrados de dx y dy.

¿Cuál es el propósito de transformar la integral en términos de la variable t?

Transformar la integral en términos de la variable t permite trabajar con funciones paramétricas para x y y, facilitando el cálculo de la integral sobre la curva. Esto se logra al expresar las derivadas de x y y con respecto a t, y luego reemplazarlas en la integral.

¿Por qué se multiplica y divide por dt en el proceso de transformación algebraica?

Multiplicar y dividir por dt es una técnica algebraica que permite incluir la variable t en la integral de manera coherente. Esto facilita el cálculo al expresarlo completamente en términos de t, lo que es crucial para evaluar la integral en un sistema de coordenadas paramétricas.