Determine internal resultant loading | 1-22 | stress | shear force | Mechanics of materials rc hibb
Summary
TLDRThis educational video tackles problem 1-22 from 'Mechanics of Material' by RC Hibler, focusing on stress analysis. It guides viewers through calculating reactive forces at a pin and link BC of a metal structure under a 120 Newton force. The video then explains how to determine the internal loading on a cross-section at point D. Using equilibrium equations and geometrical analysis, the presenter solves for various forces and moments, offering a clear understanding of mechanics in materials.
Takeaways
- 🔧 The problem is from 'Mechanics of Material' by RC Hibler, specifically chapter 1 on stress.
- 📐 A 120 Newton force is applied to a metal structure punch, and the task is to determine the reactive forces at pin A and link BC.
- 🔍 To find the reaction force at pin A, the structure is analyzed using equilibrium equations, considering moments about point A.
- 📏 The reaction force at pin A is calculated by resolving the forces into horizontal (ax) and vertical (ay) components.
- 📐 The force in link BC (FBC) is found to be 13856 Newtons or approximately 13.86 kN using the equilibrium equations.
- 🔄 The vertical reaction force at point A (ay) is determined to be 14.89 Newtons or 1.49 kN, considering the vertical components of the forces.
- 🔄 The horizontal reaction force at point A (ax) is calculated to be 60 Newtons using the equilibrium of forces in the horizontal direction.
- 📐 The resultant reaction force at pin A is calculated using the Pythagorean theorem, yielding approximately 1.49 kN.
- 🔍 For the internal loading at cross-section D, the structure is sectioned, and a free body diagram is used to determine the normal force (ND), shear force (VD), and bending moment (MD).
- 📏 The internal loading at point D is found with ND being 120 Newtons, VD being 0 Newtons, and MD being 36 Newton-meters, indicating the forces and moments acting on the structure at that point.
Q & A
What is the force applied on the metal sturred punch handle?
-The force applied on the handle is 120 Newtons.
What are the two components of the reaction force at point B when link BC is removed?
-The two components of the reaction force at point B are the horizontal component (FBCx) and the vertical component (FBCy).
How is the angle of 30° used in determining the components of FBC?
-The angle of 30° is used to calculate the horizontal and vertical components of the reaction force FBC using trigonometric functions, specifically cosine and sine.
What is the magnitude of the reaction force FBC in the link BC?
-The magnitude of the reaction force FBC is approximately 13856 Newtons or 13.85 Kilo-Newtons when rounded.
What are the equations of equilibrium used to find the reaction forces at point A?
-The equations of equilibrium used are the sum of all forces along the y-direction and the sum of all forces along the x-direction, which must equal zero.
What is the vertical reaction force (ay) at point A?
-The vertical reaction force (ay) at point A is approximately 14.89 Newtons or 1.49 Kilo-Newtons.
What is the horizontal reaction force (ax) at point A?
-The horizontal reaction force (ax) at point A is 60 Newtons.
How is the resultant reaction force at point A calculated?
-The resultant reaction force at point A is calculated using the Pythagorean theorem by combining the horizontal and vertical components (ax and ay).
What is the internal loading acting on the cross-section at point D?
-The internal loading at point D includes the normal force (ND), shear force (VD), and bending moment (MD).
What are the values of ND, VD, and MD at point D?
-The values are ND = 120 Newtons, VD = 0 Newtons, and MD = 36 Newton-meters.
How is the bending moment (MD) at point D calculated?
-The bending moment (MD) at point D is calculated by considering the moment due to the 120 Newton force at a perpendicular distance of 0.3 meters from point D.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Mechanics of Solids Interview Questions
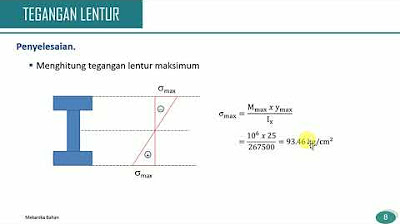
Mekanika Bahan - Tegangan Lentur

What is Mechanics of Materials and why it is important in engineering?

Irisan Kerucut - Elips • Part 11: Contoh Soal Persamaan Garis Singgung Elips

18A Advanced Strength of Materials - Spheres in Contact

Transformasi Tegangan (Part 1) - Mekanika Material / Kekuatan Material
5.0 / 5 (0 votes)
