18A Advanced Strength of Materials - Spheres in Contact
Summary
TLDRThis lecture delves into the mechanics of contact between two bodies of material, focusing on the stress produced by contact. It introduces the concept of Hertz contact stress, which is crucial for understanding the deformation and stress distribution in scenarios like spacecraft reaction wheels, bearings, and gears. The speaker emphasizes the use of closed-form solutions for practical applications, detailing the assumptions made for linear elasticity, isotropic materials, and frictionless contact. Key equations for contact area, pressure, and stress distribution are presented, highlighting their dependence on material properties and applied force.
Takeaways
- 📚 The lecture focuses on the contact of bodies, specifically the stresses produced by the contact between two bodies of materials.
- 🔍 It begins with an introduction to the theory of elasticity, including the governing equations and strain-deflection relationships, with a total of 15 equations for 15 unknowns.
- 🧩 The use of finite elements is mentioned as a common approach to solve such problems, but it's noted that analytical solutions are often more practical for certain applications.
- 📐 The course aims to provide handy analytical solutions for real-world applications, as opposed to relying solely on finite element methods.
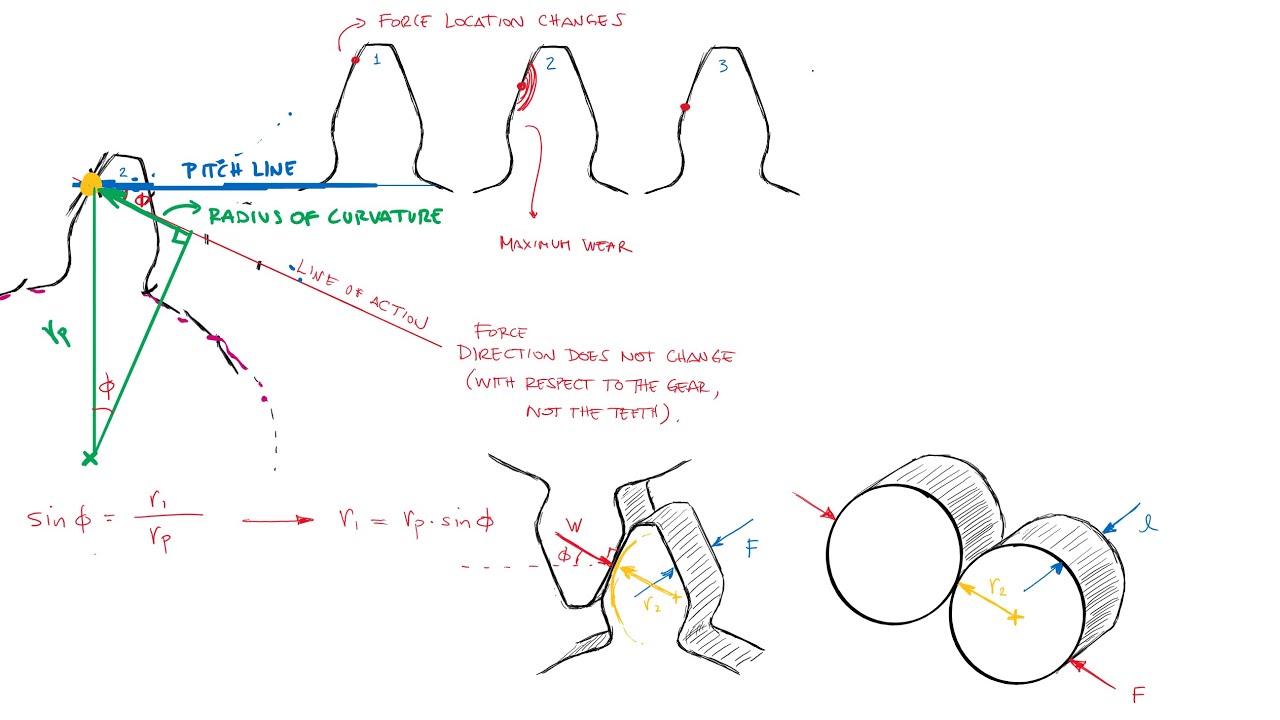
- 🔨 External loads, in this context, are the forces exerted by two bodies of materials coming into contact, which in turn produce internal loads within the materials.
- 🔍 Several assumptions are made for the theoretical model, including isotropic materials, linear elastic properties, small contact areas relative to body radii, and smooth contact surfaces without asperities.
- 💡 The Hertz contact theory is introduced, which deals with the stress distribution in spheres when they come into contact, considering elastic deformation and avoiding infinite stress scenarios.
- 🛰️ Applications of contact stress theory are highlighted, such as in spacecraft control systems, bearings, and gears, where contact forces are significant.
- 📉 The script provides formulas for calculating the contact area, maximum contact pressure, and the displacement of the center of spheres when two bodies come into contact.
- 📏 The principal stresses and maximum shear stress are calculated using specific formulas that consider the force applied, the Poisson's ratio, and the depth within the material.
- 🔑 The importance of understanding these stresses is emphasized for predicting material failure and ensuring that stresses do not exceed material yield limits.
Q & A
What is the primary focus of the course discussed in the transcript?
-The primary focus of the course is to look at closed-form solutions for contact mechanics problems, which can be used in real-world applications where finite elements may not be the best approach.
What are the three governing equations of elasticity mentioned in the script?
-The script does not provide specific details about the three governing equations of elasticity, but it implies that they are fundamental in solving problems related to contact between bodies of materials.
How many strain-deflection relationships are there in the context of the script?
-There are six strain-deflection relationships mentioned in the script, which, along with the three governing equations, make up a total of 15 equations used to solve contact problems.
What are the assumptions made when analyzing the contact between two bodies of material?
-The assumptions include: the bodies of material are isotropic, they remain under linear elastic properties, the contact area is small relative to the radii of the contacting bodies, the contacting bodies are smooth, the strains are small, and the bodies come into contact in a frictionless manner.
What is the significance of the Hertz contact theory in the context of the script?
-The Hertz contact theory is significant as it provides a method to calculate the stress distribution when two bodies, such as spheres, come into contact. It helps to understand the elastic deformation and the contact area that forms between the bodies.
Why might closed-form solutions be preferred over finite element methods in certain applications?
-Closed-form solutions may be preferred when the fidelity needed in the model is high, and quick answers are required. They can be more practical for certain problems where finite element methods may be too complex or time-consuming.
What is the relationship between the contact area and the force applied to two spheres in contact?
-The contact area is directly related to the force applied to the spheres. As more force is applied, the contact area increases, and this relationship is described by a formula involving the force, the moduli of elasticity, and the radii of the spheres.
What is the formula for calculating the maximum contact pressure between two spheres?
-The maximum contact pressure is given by the formula \( P_{max} = \frac{3F}{2\pi a^2} \), where \( F \) is the force applied and \( a \) is the radius of the contact area.
How is the displacement of the center of the spheres calculated when in contact?
-The displacement of the center of the spheres is calculated using a formula that depends on the force applied, the moduli of elasticity, and the radii of the spheres, but the exact formula is not provided in the script.
What are the formulas for calculating the principal stresses and the maximum shear stress in the contact area?
-The principal stresses are calculated using a formula that depends on the depth \( Z \), the radius \( a \), the Poisson's ratio, and the force applied. The maximum shear stress is the absolute value of half the difference between the highest and lowest principal stresses.
Why is it important to calculate the stresses generated during contact between materials?
-Calculating the stresses is important to ensure that the materials do not exceed their yield strength, which could lead to failure or damage. It helps in predicting the structural integrity and performance under contact conditions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)