Transformasi Tegangan (Part 1) - Mekanika Material / Kekuatan Material

Summary

This lecture focuses on material strength mechanics, specifically on stress transformation. The professor revisits concepts from previous lessons, such as combined stress, and introduces stress transformation, including principal stresses (Sigma 1 and Sigma 2) and maximum shear stress (Tao Max). The methods discussed to compute these stresses are through formulas or the Mohr's Circle diagram. Students are encouraged to understand how to calculate and visualize these stress transformations effectively. The session emphasizes the importance of calculating the stress state before applying stress transformations and highlights two methods for solving problems: using formulas or Mohr's Circle diagrams.

Takeaways

• 😀 The lecture focuses on the concept of 'stress transformation' in material strength mechanics, specifically dealing with principal stresses and shear stresses.
• 😀 The key topic of this session is 'Transformasi Tegangan' (Stress Transformation), which involves determining the principal stresses (Sigma 1, Sigma 2) and maximum shear stress (Tau Max).
• 😀 There are two main methods for calculating stress transformation: using formulas and using Mohr's Circle diagram.
• 😀 The transformation of stress can be calculated using a formula, which includes terms for the normal stresses (Sigma X, Sigma Y) and shear stress (Tau XY).
• 😀 Another approach is to use Mohr's Circle, a graphical method to visually determine the principal stresses and maximum shear stress.
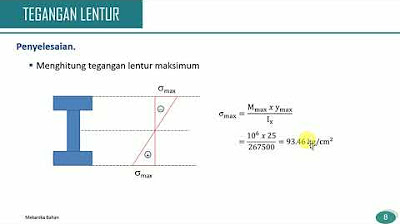
• 😀 In the previous session (Chapter 6), students learned about combined stresses and how to calculate the combined normal and shear stresses (Sigma X, Sigma Y, Tau XY).
• 😀 The normal stresses and shear stress can be derived from the combined stress values, which are then used in the transformation formulas or Mohr's Circle diagram.
• 😀 The principal stress values (Sigma 1 and Sigma 2) are obtained by inputting stress values into the transformation formula, which involves basic algebraic manipulation.
• 😀 Mohr's Circle allows for a graphical determination of Sigma 1 (maximum principal stress), Sigma 2 (minimum principal stress), and Tau Max (maximum shear stress).
• 😀 It is emphasized that to perform a stress transformation, the stress state (Sigma X, Sigma Y, Tau XY) must first be established from the combined stresses before applying any transformation methods.
• 😀 In conclusion, understanding stress transformation is crucial for analyzing the behavior of materials under different loading conditions, and both formula-based and graphical methods are valuable tools for engineers.

Q & A

What is the main topic of this lecture?

The main topic of this lecture is stress transformation, specifically focusing on calculating principal stresses (Sigma 1 and Sigma 2) and maximum shear stress (tau Max) using two methods: formulas and Mohr's Circle.

What are the two methods mentioned for calculating stress transformation?

The two methods for calculating stress transformation are: 1) using formulas, and 2) using Mohr's Circle (a graphical method).

What is the significance of Sigma 1 and Sigma 2 in stress transformation?

Sigma 1 and Sigma 2 represent the principal stresses, which are the normal stresses acting on a material at a point, in the directions where shear stress is zero.

How do you calculate the maximum shear stress (tau Max)?

The maximum shear stress (tau Max) can be calculated using the formula: tau Max = sqrt(((Sigma X - Sigma Y) / 2)^2 + tau XY^2), where Sigma X and Sigma Y are normal stresses, and tau XY is the shear stress.

What is Mohr's Circle, and how is it used in stress transformation?

Mohr's Circle is a graphical method used to determine principal stresses and maximum shear stress. It involves plotting normal and shear stresses on a circle, where the principal stresses are located at the extremes, and the maximum shear stress corresponds to the radius of the circle.

How can you determine the principal stresses from Mohr's Circle?

The principal stresses (Sigma 1 and Sigma 2) can be determined by identifying the points on the Mohr's Circle that represent the maximum and minimum normal stresses, which are located at the right and left extremes of the circle.

What does the lecture say about calculating stress in two dimensions?

In this lecture, the stress analysis is conducted in two dimensions, where the normal stresses (Sigma X and Sigma Y) and shear stress (tau XY) are considered, and the corresponding transformations are calculated.

Why is it important to first obtain the stress state before transforming the stresses?

It is important to first determine the stress state because the stress transformation relies on knowing the initial normal and shear stresses. Once the stress state is known, the transformation to principal and shear stresses can be calculated.

How does the formula for calculating Sigma 1 differ from that for Sigma 2?

The formula for calculating Sigma 1 involves adding the normal stresses (Sigma X + Sigma Y) and the square root term, while the formula for Sigma 2 involves subtracting Sigma X and Sigma Y. The only difference is the sign between the normal stresses in the formula.

What key conclusion does the lecturer make at the end of the lecture?

The key conclusion is that in order to perform stress transformation, the stress state must first be determined. The transformation involves finding the principal stresses and maximum shear stress, and this can be done using either the formula method or Mohr's Circle.