3 Método de Eliminación
Summary
TLDREl video ofrece una explicación detallada del método de eliminación para resolver sistemas de ecuaciones lineales con dos incógnitas. Se discute la importancia de elegir la variable a eliminar y cómo manipular las ecuaciones para cancelarla, utilizando el coeficiente numérico. Se presentan dos ejemplos, uno con doble eliminación y otro con coeficientes distintos, para demostrar técnicas específicas de eliminación. El objetivo es encontrar el par de soluciones para cada sistema, mostrando paso a paso cómo llegar a las soluciones x, y.
Takeaways
- 📚 El video trata sobre cómo resolver sistemas de ecuaciones lineales con dos incógnitas utilizando el método de eliminación.
- 🔄 El método de eliminación implica intercambiar ecuaciones o manipularlas para eliminar una variable de manera sistemática.
- 🔢 Es importante que el coeficiente de la variable a eliminar sea distinto de cero para poder aplicar el método de eliminación.
- ⚖️ Se puede utilizar la 'doble eliminación' cuando las ecuaciones son muy similares y los coeficientes numéricos son fácilmente manipulables.
- 🤔 Al elegir qué variable eliminar, se debe considerar el coeficiente numérico asociado y realizar la operación apropiada para cancelar esa variable.
- ➕/➖ Se pueden sumar o restar ecuaciones para eliminar una variable, dependiendo de los signos de los coeficientes.
- 🔄 En el primer ejemplo, se utiliza la doble eliminación para eliminar ambas variables 'x' e 'y', encontrando así la solución.
- 📉 El segundo ejemplo muestra cómo manejar un sistema donde los coeficientes y constantes son distintos, requiriendo una multiplicación y sumación cuidadosa para eliminar.
- 📈 Se resalta la importancia de nombrarlas las ecuaciones antes de manipulularlas, para no perderse en el proceso de eliminación.
- 📌 Al resolver el segundo sistema, se muestra cómo encontrar ecuaciones equivalentes para poder eliminar variables de manera efectiva.
- 📝 Finalmente, el video resalta que el método de eliminación es una herramienta poderosa para resolver sistemas de ecuaciones lineales, y el proceso puede variar según la configuración de las ecuaciones.
Q & A
¿Qué método se utiliza para resolver los sistemas de ecuaciones lineales en el video?
-El método utilizado para resolver los sistemas de ecuaciones lineales en el video es el método de eliminación.
¿Cuál es el primer paso para usar el método de eliminación en un sistema de ecuaciones lineales de segundo orden?
-El primer paso es intercambiar cualquiera de las dos ecuaciones del sistema y decidir qué variable queremos eliminar, teniendo en cuenta el coeficiente numérico que acompaña a esa variable.
¿Por qué es importante que la constante multiplicada a la ecuación para eliminar una variable sea distinta de cero?
-Es importante que la constante sea distinta de cero para asegurarnos de que la operación de eliminación sea efectiva y no resulte en una ecuación trivial o sin sentido.
¿Qué se denomina 'doble eliminación' y cómo se aplica en el primer ejemplo del video?
-La 'doble eliminación' se refiere a la técnica de eliminar ambas variables en el sistema de ecuaciones, sumando o restando ecuaciones para cancelar una variable y luego resolviendo para la otra. En el primer ejemplo, se usó para eliminar las 'y' y encontrar la solución para 'x'.
En el primer ejemplo, ¿cómo se determinó la variable que se eliminaría primero?
-Se determinó observando que las ecuaciones eran muy similares y la diferencia estaba en el signo de la variable 'y', por lo que se decidió eliminar 'y' primero.
¿Cómo se resuelve la ecuación '2y es igual a 4' para encontrar el valor de 'y'?
-Para resolver '2y = 4', se divide ambos lados de la ecuación por 2, resultando en 'y = 2'.
En el segundo sistema de ecuaciones, ¿cómo se identifican las ecuaciones equivalentes para la eliminación?
-Se multiplican las ecuaciones originales por coeficientes que permitan que las variables a eliminar tengan el mismo coeficiente en ambas, permitiendo su eliminación al sumar o restar las ecuaciones.
¿Cuál es la ventaja de usar el método de doble eliminación en el segundo sistema de ecuaciones del video?
-La ventaja es que permite resolver el sistema de ecuaciones de manera más eficiente, evitando la necesidad de realizar sustituciones adicionales y直奔解。
¿Cómo se determina el valor de 'x' en el segundo sistema de ecuaciones utilizando el método de eliminación?
-Se suman las ecuaciones equivalentes para eliminar la variable 'y', resultando en una ecuación sencilla en 'x', y se resuelve para encontrar que 'x' es igual a un tercio.
En el segundo sistema, ¿qué estrategia se usa para eliminar la variable 'x' y encontrar el valor de 'y'?
-Se restan las ecuaciones equivalentes para eliminar 'x', resultando en una ecuación sencilla en 'y', y se resuelve para encontrar que 'y' es igual a menos un sexto.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Matemáticas Video 2 8

✅ Sistema de Ecuaciones Lineales [ Método de Eliminación ] - Ejemplos Resueltos #1

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

COMO RESOLVER UN SISTEMAS DE ECUACIONES DE 2X3/METODO DE REDUCCION
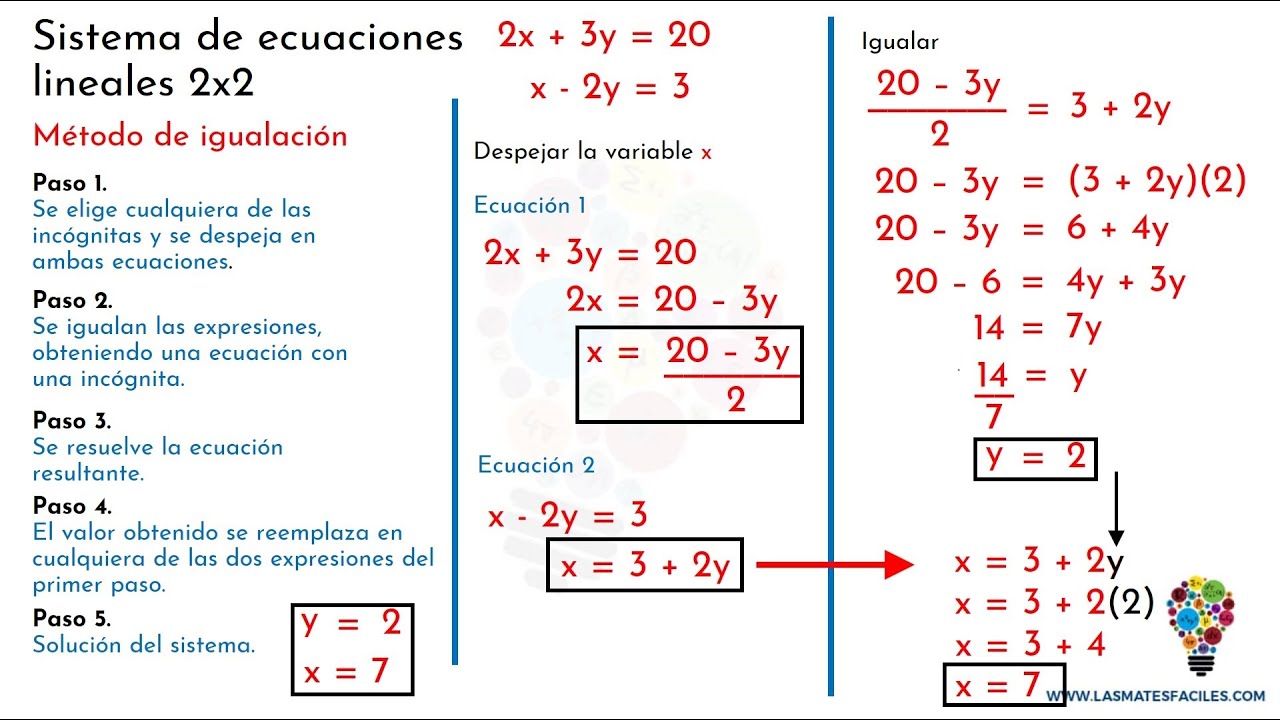
Sistemas de Ecuaciones 2x2 - Método de Igualación

▷ Сómo resolver un sistema de ecuaciones por el MÉTODO DE GAUSS JORDAN paso a paso
5.0 / 5 (0 votes)