Funciones Trigonométricas - Características Generales

Summary

Este video explica cómo las funciones trigonométricas, como el seno y el coseno, se aplican en situaciones reales como el movimiento de cuerdas, las mareas, la vibración de guitarras y el movimiento de una noria. A través del círculo unitario, se derivan estas funciones para representar gráficamente fenómenos periódicos. Se destacan las características clave de las gráficas de seno y coseno, como su periodicidad, amplitud, y simetría. Además, se explica cómo estas funciones infinitas se repiten a medida que continúan, proporcionando una visión clara de su comportamiento en el plano cartesiano.

Takeaways

• 😀 El movimiento de una cuerda vibrante genera una onda periódica, similar a las funciones trigonométricas.
• 😀 El modelo de la función trigonométrica puede aplicarse a situaciones reales como la salida del sol, las mareas o las cuerdas de guitarra.
• 😀 El nivel de las mareas y la vibración de cuerdas de guitarra pueden representarse mediante funciones trigonométricas como seno o coseno.
• 😀 El movimiento de una noria puede describirse mediante una función trigonométrica, registrando la altura de un punto a lo largo del tiempo.
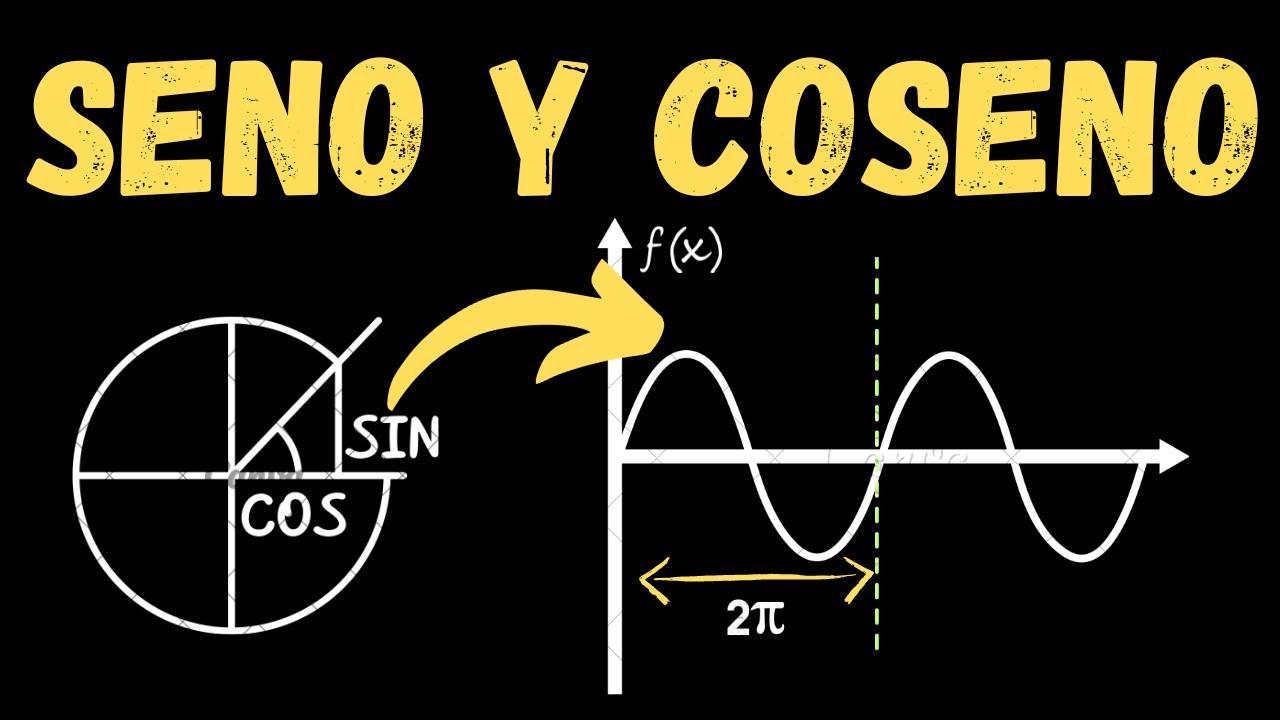
• 😀 Para representar gráficamente una función seno o coseno, se utiliza el círculo unitario, donde el radio tiene valor 1.
• 😀 La función seno está relacionada con el cateto opuesto al ángulo en el círculo unitario, y su gráfica oscila entre -1 y 1.
• 😀 La función coseno se relaciona con el cateto adyacente al ángulo en el círculo unitario, y su gráfica también oscila entre -1 y 1.
• 😀 Las gráficas de las funciones seno y coseno tienen un periodo de 360 grados, lo que significa que se repiten infinitamente.
• 😀 El eje principal de las gráficas de las funciones trigonométricas es la línea horizontal que pasa por el origen, representando el valor 0.
• 😀 Las funciones seno y coseno son funciones periódicas, lo que significa que sus valores se repiten después de un intervalo específico, el periodo.

Q & A

¿Qué aplicaciones reales tienen las funciones trigonométricas?

Las funciones trigonométricas se aplican en situaciones reales como el movimiento de cuerdas, el nivel de las mareas, el horario de salida del sol, las vibraciones de cuerdas de guitarra, y el movimiento de una noria, entre otras.

¿Cómo se puede modelar el movimiento de una noria mediante una función trigonométrica?

El movimiento de una noria se puede modelar mediante una función trigonométrica al registrar la altura de un punto en el asiento de la noria en intervalos de tiempo iguales. Esta altura sigue un patrón periódico, similar al de una función seno o coseno.

¿Por qué se utiliza el círculo unitario para representar las funciones trigonométricas?

El círculo unitario se utiliza para simplificar la representación de las funciones trigonométricas, ya que su radio es 1, lo que facilita los cálculos y la visualización de las funciones seno y coseno.

¿Cómo se representa el seno en el círculo unitario?

En el círculo unitario, el seno de un ángulo se representa como la distancia vertical (cateto opuesto) desde el origen hasta el punto sobre el círculo. Esta distancia es la coordenada y del punto.

¿Cuál es la característica principal de la función seno en su gráfica?

La función seno tiene un periodo de 360 grados, con una amplitud de 1, lo que significa que su valor oscila entre -1 y 1. Su gráfica es infinita y repite el mismo patrón de forma periódica.

¿Cómo se define el periodo y la amplitud de una función trigonométrica?

El periodo de una función trigonométrica es el tiempo o el ángulo necesario para que la función complete un ciclo completo. La amplitud es la distancia máxima entre el valor más alto y el valor más bajo de la función, que en el caso del seno y el coseno es 1.

¿Qué diferencia existe entre la gráfica de la función seno y la de la función coseno?

La gráfica de la función seno comienza en cero, sube hasta 1, baja hasta -1, y vuelve a cero. En cambio, la función coseno comienza en 1, baja hasta -1, sube nuevamente hasta 1, y termina en 1, con un desplazamiento horizontal respecto a la función seno.

¿Cómo se describe el movimiento de una cuerda vibrando en términos de una función trigonométrica?

Cuando una cuerda vibrante se mueve verticalmente, genera una onda cuyo movimiento es periódico. Este movimiento puede representarse mediante una función trigonométrica, con el eje principal siendo el momento en que la cuerda está en reposo.

¿Qué significa que una función trigonométrica sea infinita?

Que una función trigonométrica sea infinita significa que su gráfica se repite de manera indefinida. Por ejemplo, la función seno o coseno sigue repitiendo su patrón a medida que el ángulo aumenta o el tiempo transcurre.

¿Qué importancia tiene el eje principal en las gráficas de funciones trigonométricas?

El eje principal es una línea horizontal que pasa por el centro de la gráfica de la función trigonométrica, representando el valor cero. Este eje divide la gráfica en dos partes simétricas, y su existencia permite observar cómo la función oscila alrededor de este valor.