Fungsi Transenden 3 (Fungsi Eksponensial Natural)
Summary
TLDRThis educational video covers the concept of natural exponential functions (EXP), explaining their relation to logarithmic functions (LN) as their inverse. It dives into the mathematical foundations of exponential functions, using the number 'e' (approximately 2.71828) to demonstrate its applications in real-world phenomena like population growth and bank interest. The video also highlights the key properties of exponential functions, such as their derivatives and integrals, and explains various methods for solving related problems, including differentiation and integration with substitution techniques. Overall, the content aims to deepen understanding of the significance and use of natural exponential functions in calculus.
Takeaways
- 😀 The natural exponential function (EXP) is the inverse of the natural logarithm (LN).
- 😀 The relationship between LN and EXP can be represented as LN(x) = y and EXP(y) = x.
- 😀 The base of the natural exponential function is the constant 'e', approximately equal to 2.718281828.
- 😀 The number 'e' was discovered by Leonhard Euler and is used in various natural phenomena such as population growth and bacterial growth.
- 😀 The natural exponential function has key properties similar to exponential functions, such as e^a * e^b = e^(a+b).
- 😀 The derivative of e^x is e^x itself, making it a special and unique function in calculus.
- 😀 The integral of e^x is also e^x + C, where C is the constant of integration.
- 😀 The natural exponential function is used to model growth processes such as bank interest and population dynamics.
- 😀 The function e^x has a graph that is a reflection of the graph of y = x.
- 😀 Euler's number 'e' is an irrational number, similar to the mathematical constant pi (π), which also relates to geometric shapes.
- 😀 An example of applying the chain rule in differentiation shows how e^(x² + x) is differentiated, combining exponential and polynomial derivatives.
Q & A
What is the natural exponential function (EXP)?
-The natural exponential function, denoted as EXP, is the inverse of the natural logarithm function (LN). It can be expressed as y = e^x, where e is a constant approximately equal to 2.718281828.
How is the natural exponential function related to the natural logarithm function?
-The natural exponential function (EXP) is the inverse of the natural logarithm function (LN). This means that if y = LN(x), then x = e^y. In other words, LN(x) and EXP are mathematical inverses of each other.
What is the significance of the constant 'e' in the natural exponential function?
-The constant 'e' is a mathematical constant that is approximately equal to 2.718281828. It is fundamental in mathematics and appears naturally in various areas such as population growth, bank interest calculations, and certain physical phenomena.
What are some real-world applications of the natural exponential function?
-The natural exponential function is used in real-world applications like population growth modeling, compound interest calculations, and bacterial growth. It helps in understanding processes that grow or decay exponentially over time.
What is the graph of the natural exponential function y = e^x like?
-The graph of y = e^x is a smooth curve that increases rapidly as x increases. It is always above the x-axis and approaches zero as x becomes more negative. The graph is asymptotic to the x-axis as x tends to negative infinity.
What is the derivative of the natural exponential function?
-The derivative of the natural exponential function e^x is e^x itself. This means that if f(x) = e^x, then f'(x) = e^x.
How do you integrate the natural exponential function?
-The integral of e^x with respect to x is simply e^x + C, where C is the constant of integration.
What is the rule for multiplying two exponential functions with the same base?
-When two exponential functions with the same base are multiplied, the result is e^(a+b), where a and b are the exponents. In other words, e^a * e^b = e^(a+b).
What is the process for differentiating a function of the form e^(x² + x)?
-To differentiate e^(x² + x), you apply the chain rule. The derivative of e^(something) is e^(something) multiplied by the derivative of the exponent. So, the derivative of e^(x² + x) is e^(x² + x) * (2x + 1).
How does the substitution method work in integration of exponential functions?
-In integration using substitution, you substitute a part of the function with a new variable (u). Then, you differentiate u with respect to x to simplify the integral. For example, if you integrate 6e^(1/x) / x², you might substitute u = 1/x to simplify the integral.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Lec 52 - Logarithmic Functions
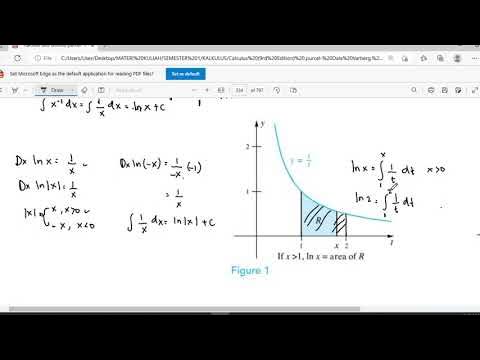
Fungsi Transenden 1 (Logaritma Natural/Ln)

Logarithmic Functions | Transforming Logarithmic Equation to Exponential Form and Vice Versa

3ª SÉRIE - ENSINO MÉDIO - FASE 2 - DESAFIO CRESCER - MATEMÁTICA

Logaritmo: Introdução Parte 1 (Aula 1 de 14)

KALKULUS | FUNGSI TRANSENDEN | LOGARITMA ASLI (Turunan dan Integral)
5.0 / 5 (0 votes)
