3ª SÉRIE - ENSINO MÉDIO - FASE 2 - DESAFIO CRESCER - MATEMÁTICA
Summary
TLDRIn this lesson, Professor Beto teaches the concept of logarithmic functions, explaining their relationship with exponential functions. Through student questions, the professor explores how logarithms are the inverse of exponents, showing step-by-step examples of calculating logarithms and their corresponding exponents. The video also explains how the graphs of logarithmic and exponential functions are symmetrical and what distinguishes them, including their increasing and decreasing behaviors based on the base value. With clear illustrations and real-world applications, this lesson helps viewers understand the fundamentals of logarithms and their graphical representation.
Takeaways
- 😀 The logarithmic function is the inverse of the exponential function.
- 😀 A logarithm calculates the exponent of a given base that transforms the base into a specific value.
- 😀 To calculate a logarithm, you are essentially determining the exponent of a base number that results in the given value.
- 😀 The logarithmic function formula is expressed as FX = log(x) with a base 'b'. The base must be a positive real number, but not equal to 1.
- 😀 Logarithms are used to solve equations involving exponents, such as 2^x = 8, where the logarithm of 8 in base 2 is 3.
- 😀 Logarithmic functions have specific properties depending on the base value. If the base is greater than 1, the graph of the function is increasing. If the base is between 0 and 1, the graph is decreasing.
- 😀 The graph of the logarithmic function does not touch the y-axis and passes through the point (1, 0) on the x-axis.
- 😀 The logarithmic and exponential functions are symmetric to each other when plotted on a graph, with their axis of symmetry being the line y = x.
- 😀 The inverse of an exponential function can be written as a logarithmic function with the same base.
- 😀 The relationship between logarithms and exponents is fundamental for understanding how the functions interact, with exponential functions growing, and logarithmic functions providing a way to solve for the exponents.
- 😀 When dealing with the inverse of a function, the exponent in the exponential function becomes part of the expression for the logarithmic function, with sign changes in certain cases, such as with added or subtracted constants.
Q & A
What is the relationship between logarithmic and exponential functions?
-Logarithmic functions are the inverse of exponential functions. This means that a logarithmic function can be used to find the exponent of a base that will result in a given number.
What does the term 'logarithm' refer to?
-The logarithm refers to the exponent of a base that transforms it into a given number. For example, if 2 raised to the power of 3 equals 8, the logarithm of 8 with base 2 is 3.
What is the significance of the base in a logarithmic function?
-The base in a logarithmic function is the number that is repeatedly multiplied to achieve the result. It is written as a subscript next to the logarithm symbol, such as log base 2 (log₂).
Can logarithmic functions have negative results?
-The results of a logarithmic function (logarithm) cannot be negative because the base and the result must both be positive numbers. Negative numbers are not valid for the base or the result in logarithmic calculations.
What is the general form of a logarithmic function?
-The general form of a logarithmic function is f(x) = log_b(x), where 'b' is the base, 'x' is the input, and the output is the exponent that makes b raised to that exponent equal to x.
How does the graph of a logarithmic function behave?
-The graph of a logarithmic function is a curve that passes through the point (1, 0) on the x-axis and approaches but never touches the y-axis. It is increasing if the base is greater than 1, and decreasing if the base is between 0 and 1.
What happens to the graph of a logarithmic function when the base is greater than 1?
-When the base of a logarithmic function is greater than 1, the graph is increasing. This means that as the value of x increases, the value of f(x) also increases.
What happens to the graph of a logarithmic function when the base is between 0 and 1?
-When the base is between 0 and 1, the graph of the logarithmic function is decreasing. As the value of x increases, the value of f(x) decreases.
How are the graphs of exponential and logarithmic functions related?
-The graphs of exponential and logarithmic functions are symmetric with respect to the line y = x. This means that the graph of a logarithmic function is a reflection of the corresponding exponential function over this line.
What is the rule for finding the inverse of an exponential function?
-To find the inverse of an exponential function, we replace the exponential expression with a logarithmic one, using the same base. For example, the inverse of f(x) = 2^x is f⁻¹(x) = log₂(x). If there is a constant added or subtracted in the exponent, it affects the transformation in the logarithmic function's formula.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Logaritmo: Introdução Parte 1 (Aula 1 de 14)

Logarithmic Functions | Transforming Logarithmic Equation to Exponential Form and Vice Versa

Lec 52 - Logarithmic Functions
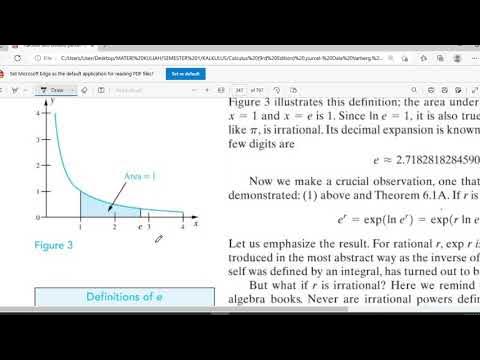
Fungsi Transenden 3 (Fungsi Eksponensial Natural)

Illustrative Math | Algebra 2 | 4.9 Lesson

(Part 1) Fungsi Logaritma Bab Fungsi dan Pemodelannya || Matematika Tingkat Lanjut Kelas XI
5.0 / 5 (0 votes)