ADIÇÃO E SUBTRAÇÃO COM RADICAIS \Prof. Gis/
Summary
TLDRThis math lesson teaches viewers how to perform operations with radicals, focusing on addition and subtraction. It explains the rule that only similar radicals—those with the same radicand and index—can be combined. The lesson includes step-by-step examples of simplifying square roots through prime factorization and shows how to decompose numbers to make radicals compatible. The teacher emphasizes understanding the basics of radical simplification and encourages reviewing previous lessons for better clarity. Viewers are motivated to subscribe and practice the material to master the topic and improve their skills in solving radical expressions.
Takeaways
- 😀 Radicals can only be added or subtracted if they are similar, meaning they must have the same radicand and the same index.
- 😀 The radicand is the number inside the square root, and the index is the root type (e.g., square root, cube root).
- 😀 Similar radicals must have the same radicand and index, regardless of the coefficients outside the radical (e.g., 5√2 and -4√2 are similar because their radicands and indices are the same).
- 😀 If the radicands are different, you cannot add or subtract the radicals directly (e.g., √2 and ∛2 are not similar because their indices are different).
- 😀 To add or subtract radicals with different radicands, you must simplify the radicands first through prime factorization.
- 😀 Prime factorization helps break down numbers into their simplest factors, making it easier to simplify the radicands and perform operations.
- 😀 If a radical expression has a coefficient outside the radical, it does not affect the similarity of the radicals when performing operations, as long as the radicands and indices match.
- 😀 When simplifying radicals, group factors that are the same, such as pairs of 2s or 3s, based on the index of the root (e.g., squares for square roots, cubes for cube roots).
- 😀 After simplifying the radicands, you can combine the terms by adding or subtracting the coefficients outside the radical, keeping the radical part the same.
- 😀 The lesson prepares students to recognize when radicals can be added or subtracted and when they need to be simplified using prime factorization before performing operations.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is performing operations with radicals, specifically focusing on how to add and subtract them.
What is the condition for radicals to be considered 'similar' for addition or subtraction?
-For radicals to be considered 'similar' and thus be added or subtracted, they must have the same radicand (the number inside the radical) and the same index (the root type, e.g., square root or cube root).
What does the term 'radicand' refer to in the context of radicals?
-The 'radicand' refers to the number inside the radical symbol. For example, in the square root of 25, 25 is the radicand.
What is the index of a radical, and how does it affect the operation with radicals?
-The index of a radical refers to the type of root, such as square root (index 2) or cube root (index 3). The index is important because only radicals with the same index can be added or subtracted.
Can you add or subtract two radicals if their coefficients are different but their radicands and indices are the same?
-Yes, you can add or subtract two radicals if their radicands and indices are the same, regardless of their coefficients. Only the coefficients are added or subtracted.
Why is it not possible to add or subtract the square root of 50 and the square root of 18 directly?
-It is not possible to add or subtract the square root of 50 and the square root of 18 directly because their radicands are different (50 and 18), so they are not considered similar.
What process can be used to simplify the radicals and make their radicands the same in the example with square roots of 50 and 18?
-To simplify the radicals, you can decompose the numbers (50 and 18) into their prime factors. This allows you to extract square factors from the radicands and possibly make them the same.
What is the significance of 'prime factorization' in simplifying radicals?
-Prime factorization is used to break down numbers into their prime factors. This helps in simplifying radicals by identifying square factors (for square roots) or cube factors (for cube roots), which can be taken out of the radical.
In the process of simplifying the expression with the square roots of 12, 75, and 48, what is the key step in identifying which factors can be simplified?
-The key step is grouping the factors into pairs that match the index of the radical. For square roots, you group the prime factors in pairs (two at a time), and for cube roots, you group them in triples.
After simplifying the radicals in the example with the square roots of 12, 75, and 48, what is the final result?
-After simplifying the radicals and combining like terms, the final result is 6 times the square root of 3 (6√3).
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

BENTUK AKAR Kelas 10 Kurikulum Merdeka

OPERATIONS ON INTEGERS

JAGO EXCELL SEKEJAP RUMUS PENJUMLAHAN, PENGURANGAN, PEMBAGIAN, DAN PERKALIAN OTOMATIS
Operazioni tra vettori in componenti cartesiane

Polinomial (Bagian 1) - Pengertian dan Operasi Aljabar Polinomial Matematika Peminatan Kelas XI
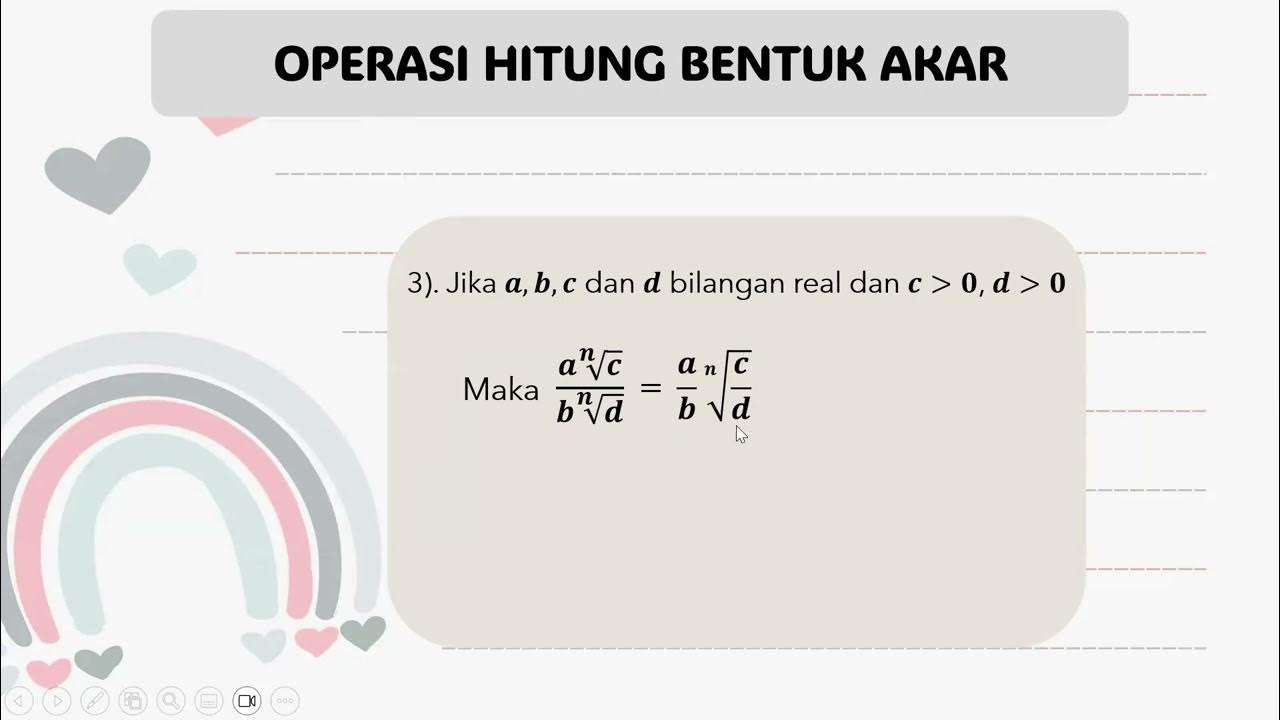
Asinkronus Topik Bentuk Akar W 2
5.0 / 5 (0 votes)
