Special Triangles (full lesson) | jensenmath.ca

Summary

This lesson on trigonometry covers essential concepts of right-angle triangles, focusing on special angles of 30°, 45°, and 60°. It reviews primary trig ratios (sine, cosine, tangent) and demonstrates their applications using SOH-CAH-TOA. The video explains how to use special triangles to find exact trig ratios without a calculator, including 45°-45°-90° and 30°-60°-90° triangles. It also walks through examples of solving for missing sides and angles, and introduces techniques for rationalizing denominators. By the end of the lesson, viewers will be equipped to solve trig problems accurately and efficiently.

Takeaways

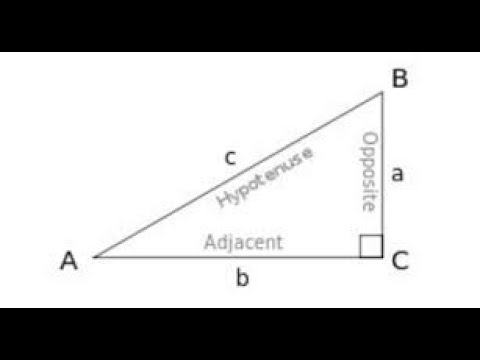
• 😀 Review of basic trigonometric ratios: Sine, Cosine, and Tangent are functions that relate angles to side lengths in right triangles. These are crucial for solving problems involving right-angle triangles.
• 😀 SOHCAHTOA acronym helps remember the trigonometric ratios: 'S' for sine (opposite/hypotenuse), 'C' for cosine (adjacent/hypotenuse), and 'T' for tangent (opposite/adjacent).
• 😀 Trigonometric ratios remain consistent for similar right triangles: Changing the size of a triangle doesn't affect the ratios of the corresponding sides, only their absolute lengths.
• 😀 The sine of 30° is always 1/2, the cosine of 30° is √3/2, and the tangent of 30° is 1/√3. These ratios are exact and don't require a calculator.
• 😀 Special triangles like the 45°-45°-90° and 30°-60°-90° triangles can be used to find exact values for trig ratios, eliminating the need for a calculator in many cases.
• 😀 In the 45°-45°-90° triangle, the sides opposite the 45° angles are equal, and the hypotenuse is √2 times the length of either leg.
• 😀 In the 30°-60°-90° triangle, the sides have a specific ratio: the side opposite 30° is half the length of the hypotenuse, and the side opposite 60° is √3/2 times the hypotenuse.
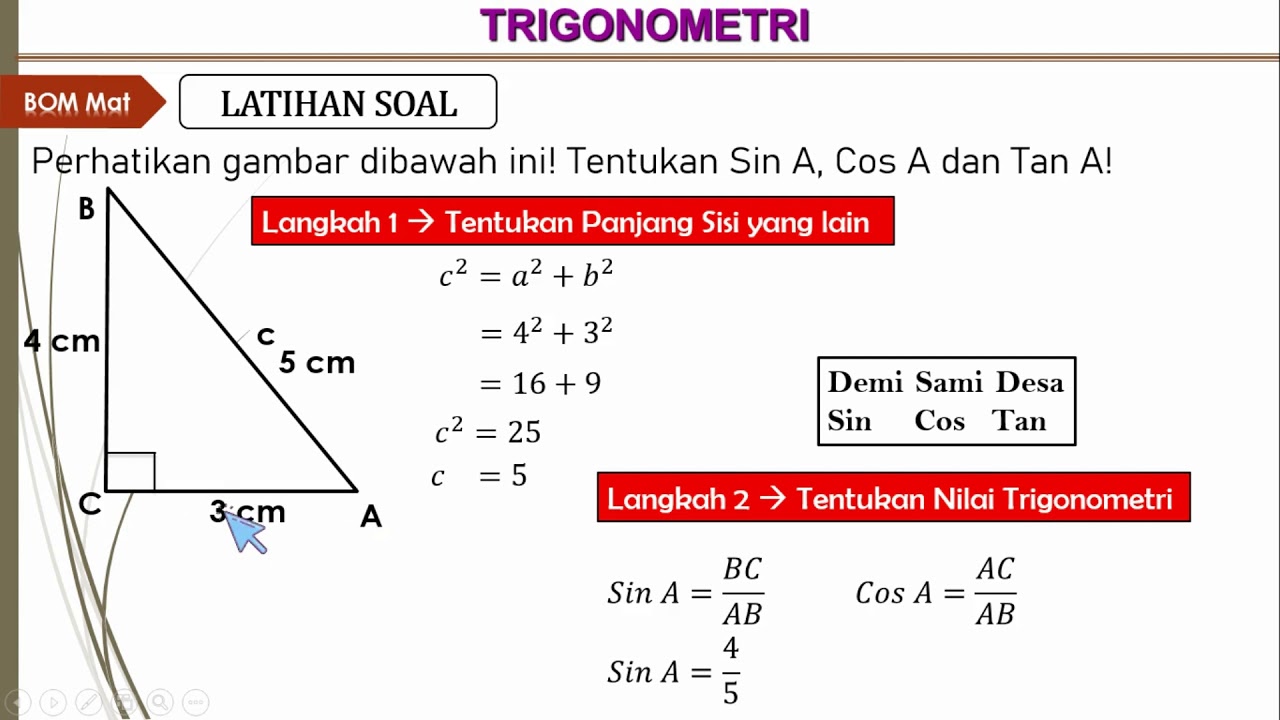
• 😀 The Pythagorean Theorem can be used to calculate the hypotenuse of a right triangle when two sides are known, and the special triangles help find exact values without a calculator.
• 😀 To find missing sides or angles in right triangles, SOHCAHTOA can be applied, with inverse functions helping to determine angles from known side ratios.
• 😀 Rationalizing denominators is important for simplifying expressions that contain square roots. This involves multiplying both the numerator and denominator by a conjugate to eliminate square roots in the denominator.

Q & A

What are the primary trigonometric ratios discussed in this lesson?

The primary trigonometric ratios discussed are sine (sin), cosine (cos), and tangent (tan). These ratios are used to relate the angles of a right triangle to the ratios of its sides.

What does the acronym SOH-CAH-TOA stand for?

SOH-CAH-TOA is a mnemonic to help remember the basic trigonometric ratios: 'S' stands for Sine = Opposite/Hypotenuse, 'C' stands for Cosine = Adjacent/Hypotenuse, and 'T' stands for Tangent = Opposite/Adjacent.

What is the significance of the 'reference angle' in trigonometry?

The reference angle is the angle in a right triangle that is used to define the trigonometric ratios. All triangles with the same reference angle are similar, meaning their corresponding side ratios are equal.

Why are trigonometric ratios for similar triangles always equivalent?

Trigonometric ratios for similar triangles are equivalent because the triangles have the same shape, and their corresponding side lengths are proportional. Therefore, the ratios of their sides are equal.

How do the special 45°-45°-90° triangles help in calculating exact trigonometric ratios?

In a 45°-45°-90° triangle, the two legs are of equal length, and the hypotenuse is equal to the leg length multiplied by √2. This allows for exact trigonometric ratios of 45° without using a calculator, such as sin(45°) = 1/√2, cos(45°) = 1/√2, and tan(45°) = 1.

What is the relationship between the sides in a 30°-60°-90° triangle?

In a 30°-60°-90° triangle, the side opposite the 30° angle is half the length of the hypotenuse, and the side opposite the 60° angle is √3/2 times the length of the hypotenuse. This triangle is derived from halving an equilateral triangle.

How can we use special triangles to calculate trigonometric ratios without a calculator?

We can use the side lengths of special triangles, like the 45°-45°-90° and 30°-60°-90° triangles, to calculate exact values for sine, cosine, and tangent ratios. These ratios are constant for the specified angles and do not require a calculator.

What is the Pythagorean theorem, and how does it apply to special triangles?

The Pythagorean theorem states that in a right triangle, the sum of the squares of the two shorter sides equals the square of the hypotenuse. It is used to find missing side lengths in right triangles, including special triangles like the 45°-45°-90° and 30°-60°-90° triangles.

What does rationalizing the denominator mean in trigonometric expressions?

Rationalizing the denominator means eliminating square roots from the denominator of a fraction. This is done by multiplying the numerator and denominator by a conjugate or suitable term that eliminates the square root.

Why is it important to rationalize the denominator in expressions like 1/√2?

Rationalizing the denominator is important because it results in a more standard form of the expression, where the denominator no longer contains a square root. This is typically considered more mathematically acceptable.