Perbandingan Trigonometri Sudut Istimewa

Summary

This video lesson introduces the topic of special angles in trigonometry, focusing on the angles 0°, 30°, 45°, 60°, and 90°. It explains how to calculate the sine, cosine, and tangent for these angles, along with their reciprocals (cosecant, secant, and cotangent). The video includes step-by-step examples, such as solving the expression sin(30°) + cos(90°) - tan(45°), and using trigonometric functions to find missing sides in right-angled triangles. The approach is clear and educational, aiming to make learning trigonometry accessible and engaging for viewers.

Takeaways

• 😀 The topic of the video is about learning trigonometry, focusing on special angles.
• 😀 The special angles discussed include 0°, 30°, 45°, 60°, and 90°.
• 😀 A table comparing trigonometric values (sin, cos, tan) for these angles is introduced.
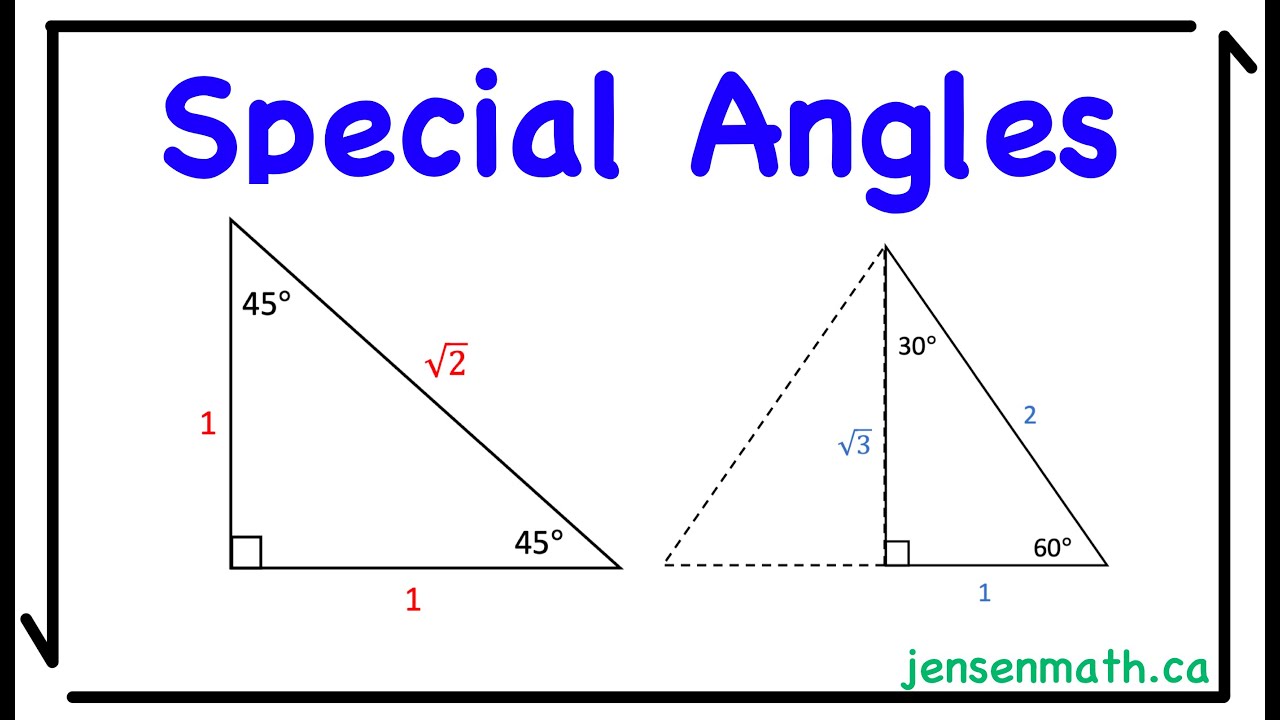
• 😀 The sine (sin) of 0° is 0, sin 30° is 1/2, sin 45° is √2/2, sin 60° is √3/2, and sin 90° is 1.
• 😀 The cosine (cos) values for the same angles are cos 0° = 1, cos 30° = √3/2, cos 45° = √2/2, cos 60° = 1/2, and cos 90° = 0.
• 😀 The tangent (tan) values are tan 0° = 0, tan 30° = 1/√3, tan 45° = 1, tan 60° = √3, and tan 90° is undefined.
• 😀 To find cosecant (csc), secant (sec), and cotangent (cot) values, simply take the reciprocal of sin, cos, and tan respectively.
• 😀 An example problem is shown to calculate the value of sin 30° + cos 90° - tan 45°, with the result being 1/2 + 0 - 1 = -1/2.
• 😀 A second example involves a right triangle with known side BC = 20 cm and angle ∠ACB = 30°. The goal is to find sides AB and AC.
• 😀 The sine and cosine functions are used to solve for the missing sides AB and AC, with AB calculated as 40 cm and AC as 20√3 cm.

Q & A

What are the special angles discussed in the lesson?

The special angles discussed in the lesson are 0°, 30°, 45°, 60°, and 90°.

What are the trigonometric functions for sine at these special angles?

The sine values for the special angles are: - sin(0°) = 0, - sin(30°) = 1/2, - sin(45°) = √2/2, - sin(60°) = √3/2, - sin(90°) = 1.

What are the cosine values for these special angles?

The cosine values for the special angles are: - cos(0°) = 1, - cos(30°) = √3/2, - cos(45°) = √2/2, - cos(60°) = 1/2, - cos(90°) = 0.

How is the tangent value calculated for these angles?

The tangent values for the special angles are: - tan(0°) = 0, - tan(30°) = 1/√3, - tan(45°) = 1, - tan(60°) = √3, - tan(90°) is undefined (as it involves division by zero).

What are the inverse trigonometric functions mentioned in the lesson?

The inverse trigonometric functions discussed are cosecant (csc), secant (sec), and cotangent (cot), which are the reciprocals of sine, cosine, and tangent respectively.

What is the formula for cosecant, secant, and cotangent?

The formulas for the inverse trigonometric functions are: - csc(θ) = 1/sin(θ), - sec(θ) = 1/cos(θ), - cot(θ) = 1/tan(θ).

In the first example, how do you solve the expression sin(30°) + cos(90°) - tan(45°)?

Using the table of values: - sin(30°) = 1/2, - cos(90°) = 0, - tan(45°) = 1. The result is: 1/2 + 0 - 1 = -1/2.

In the triangle ABC, what information is given to solve for AB and AC?

The information given includes a right triangle ABC with the right angle at C, side BC = 20 cm, and angle ABC = 30°. The goal is to find the lengths of sides AB and AC.

How do you find the length of the hypotenuse (AB) in triangle ABC?

To find AB, we use the sine function: - sin(30°) = BC/AB. From the table, sin(30°) = 1/2. So, 1/2 = 20/AB, which gives AB = 40 cm.

How do you find the length of side AC in triangle ABC?

To find AC, we use the cosine function: - cos(30°) = AC/AB. From the table, cos(30°) = √3/2. So, √3/2 = AC/40, which gives AC = 20√3 cm.