Manipulating the Trig Ratios in Geometry (example question)
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
¿Cuál es el triángulo que realmente nos interesa en este ejercicio?
-El triángulo que realmente interesa es el de la parte superior, que no es un triángulo rectángulo, aunque hay un triángulo rectángulo que lo encapsula.
¿Por qué se utiliza trigonometría de triángulos rectángulos si el triángulo no es rectángulo?
-Se utiliza la trigonometría de triángulos rectángulos porque esta proporciona herramientas universales para resolver problemas de trigonometría, incluso si el triángulo en cuestión no es rectángulo.
¿Cómo se encuentra la longitud de 'y' en este triángulo?
-Se utiliza la función tangente (tan), ya que se tiene un ángulo conocido y un lado adyacente, mientras que el lado opuesto es desconocido. La fórmula sería tan(ángulo) = opuesto/adyacente.
¿Qué triángulo trigonométrico se recomienda dibujar para recordar las relaciones trigonométricas?
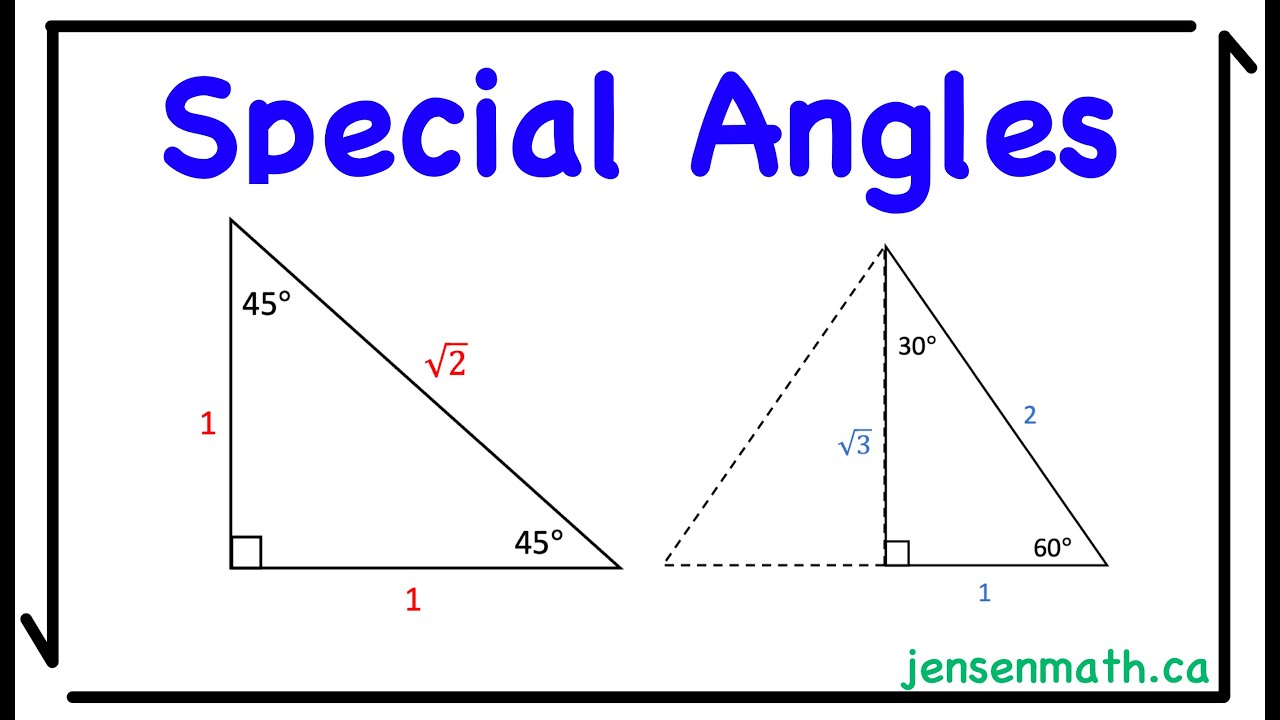
-Se recomienda dibujar los triángulos 30-60-90 y 45-45-90, ya que estos contienen las relaciones trigonométricas más fáciles de recordar.
¿Cuál es la relación trigonométrica más fácil de recordar para el ángulo de 30 grados?
-La relación trigonométrica más fácil de recordar para el ángulo de 30 grados es que el seno de 30 es 1/2.
¿Qué fórmula se utiliza para obtener las razones trigonométricas de 30, 60 y otros ángulos?
-Las fórmulas se derivan del triángulo 30-60-90. En este caso, el seno de 30 es 1/2, y se puede calcular el coseno y la tangente utilizando estas relaciones.
¿Qué ocurre cuando se utiliza el ángulo de 60 grados en el cálculo de las longitudes?
-Cuando se utiliza el ángulo de 60 grados, la tangente de 60 grados es igual a la raíz cuadrada de tres, lo que permite relacionar las longitudes de los lados del triángulo.
¿Qué sucede cuando se resuelve la ecuación con la tangente de 30 grados?
-Al resolver la ecuación utilizando la tangente de 30 grados, se multiplica por 10 para obtener la longitud de un lado, y se continúa resolviendo el problema utilizando las relaciones trigonométricas conocidas.
¿Cómo se simplifica la expresión cuando se obtiene un término con raíz cuadrada en el denominador?
-Se puede racionalizar el denominador multiplicando por la raíz cuadrada de 3 sobre sí misma, lo que elimina la raíz cuadrada del denominador.
¿Qué estrategia se recomienda para resolver este tipo de problemas de trigonometría en un examen?
-Se recomienda dibujar los triángulos clave, como los triángulos 30-60-90 y 45-45-90, y recordar las relaciones trigonométricas exactas para cada uno de los ángulos comunes. Esto facilita la resolución rápida de los problemas durante un examen.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Special Triangles (full lesson) | jensenmath.ca

Grade 10 Trigonometry: Trig Ratios Sin, Cos and Tan
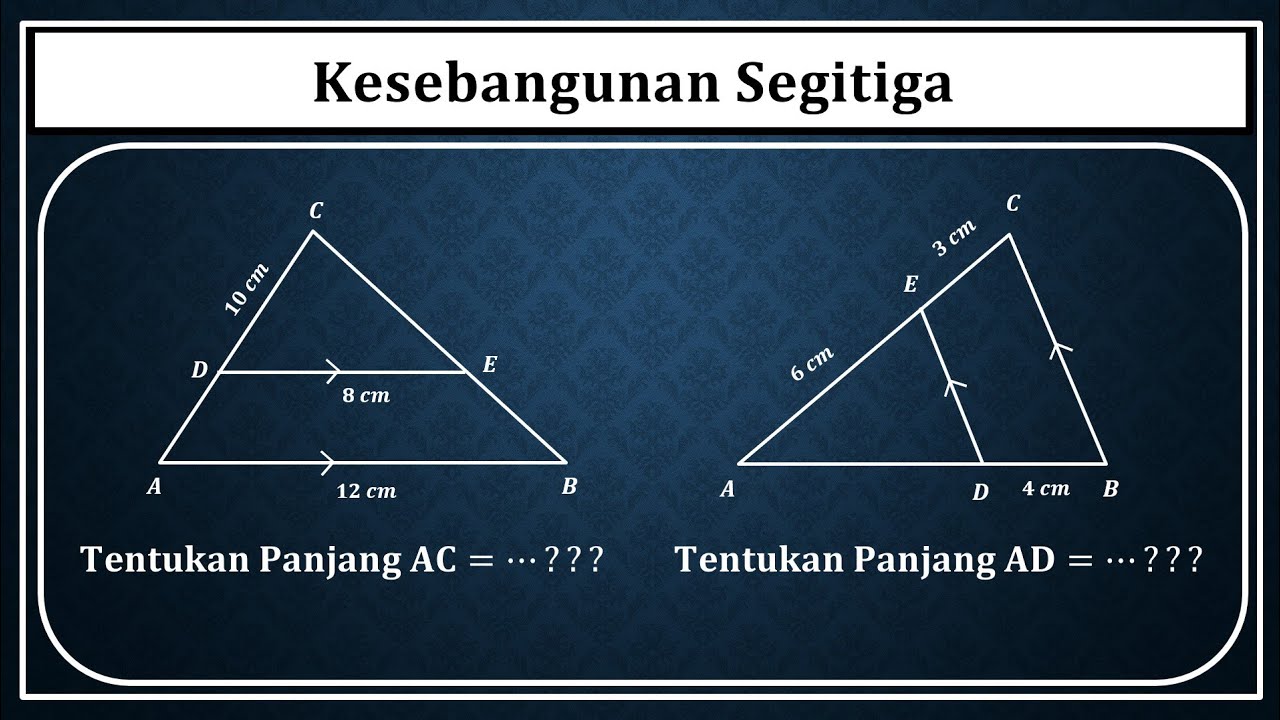
Kesebangunan segitiga

Perbandingan Senilai dan Berbalik Nilai [Part 3] - Perbandingan Berbalik Nilai

SEGITIGA ISTIMEWA SUDUT 30,60,90 DAN SUDUT 45,45,90

Teorema Pythagoras [Part 4] - Menentukan Perbandingan Sisi Segitiga Siku-siku

P3 TRIGONOMETRY (BASICS) | A LEVELS | MATHS 9709
5.0 / 5 (0 votes)