Grade 10 Trigonometry: Trig Ratios Sin, Cos and Tan

Summary

Miss Martins introduces trigonometry with a clear, friendly walkthrough of the three basic ratios—sine, cosine and tangent—using right-angled triangles. She explains how to identify the hypotenuse, opposite and adjacent sides relative to an angle, writes each trig ratio (sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/adjacent), and shares memory aids. Step-by-step examples show how to form and simplify ratios, and how to use the Pythagorean theorem to find a missing side before applying trig. The video emphasizes reasoning, simplification, and real-world relevance for Grade 10 learners.

Takeaways

• 📘 Trigonometry is a key mathematical topic introduced in Grade 10, focusing on right-angled triangles and extending into higher grades.
• 📐 Trigonometry involves finding unknown sides or angles in triangles using relationships between sides and angles.
• 🏗️ Trigonometry has many real-life applications in fields like engineering, architecture, navigation, and surveying.
• 🔺 In a right-angled triangle, the side opposite the 90° angle is always called the hypotenuse, and it is the longest side.
• 📏 The three sides of a triangle relative to a given angle are classified as the hypotenuse, the opposite side, and the adjacent side.
• 🧮 The three basic trigonometric ratios are sine (sin), cosine (cos), and tangent (tan).
• 🧠 The mnemonic ‘SOH CAH TOA’ helps remember the trig ratios: sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/adjacent.
• ✏️ When working with specific angles (like θ or β), the identification of opposite and adjacent sides depends on the position of that angle.
• 📉 Simplifying ratios (fractions) to their lowest terms is an important step when expressing trig ratios.
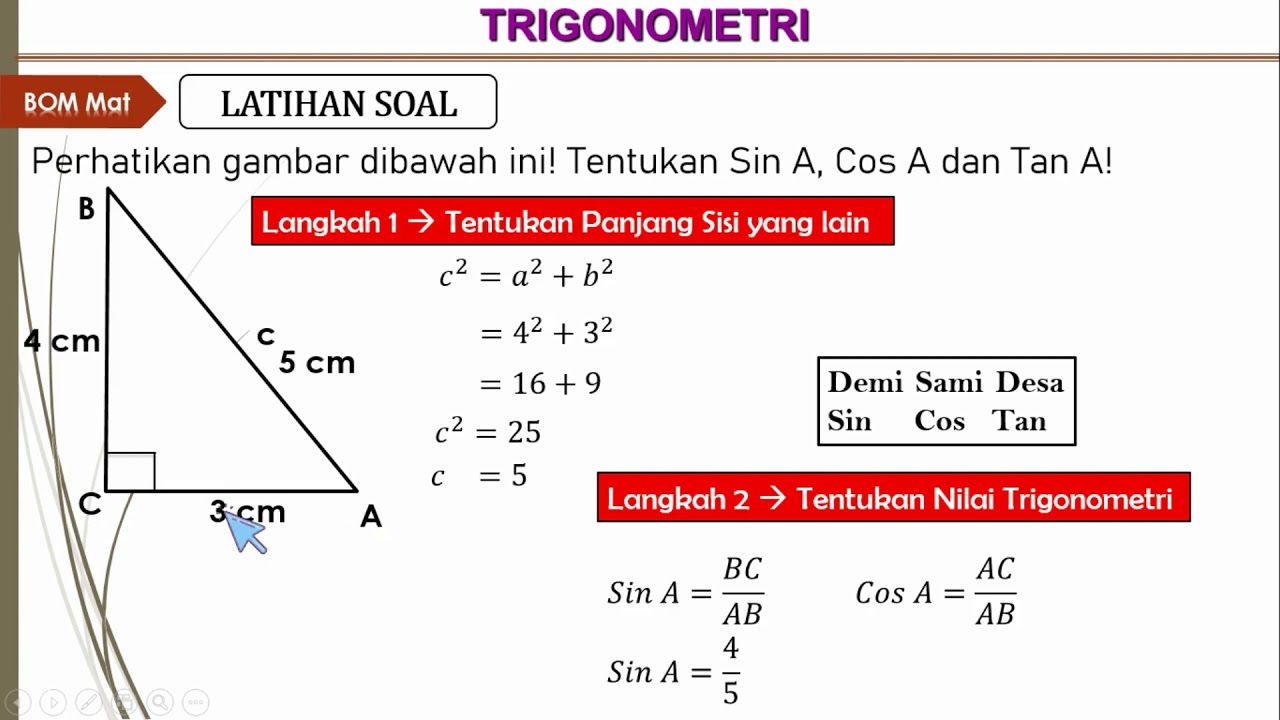
• 📊 Pythagoras’ theorem (a² + b² = c²) is used to find a missing side in a right-angled triangle before applying trigonometric ratios.
• 🧩 Examples in the lesson demonstrate how to calculate sin, cos, and tan for given triangles, emphasizing correct side identification and simplification.

Q & A

What is the main focus of the video?

The video focuses on introducing trigonometry, specifically the basic trigonometric ratios: sine (sin), cosine (cos), and tangent (tan), and how to use them in right-angled triangles.

How are trigonometric ratios used in real life?

Trigonometry has applications in fields such as engineering, architecture, navigation, and surveying. It is essential for solving problems related to triangles and angles in practical scenarios.

What defines a right-angled triangle?

A right-angled triangle is a triangle that has one angle equal to 90°. The side opposite this right angle is called the hypotenuse, which is the longest side of the triangle.

What is the hypotenuse in a right-angled triangle?

The hypotenuse is the longest side of a right-angled triangle, and it is always opposite the 90° angle.

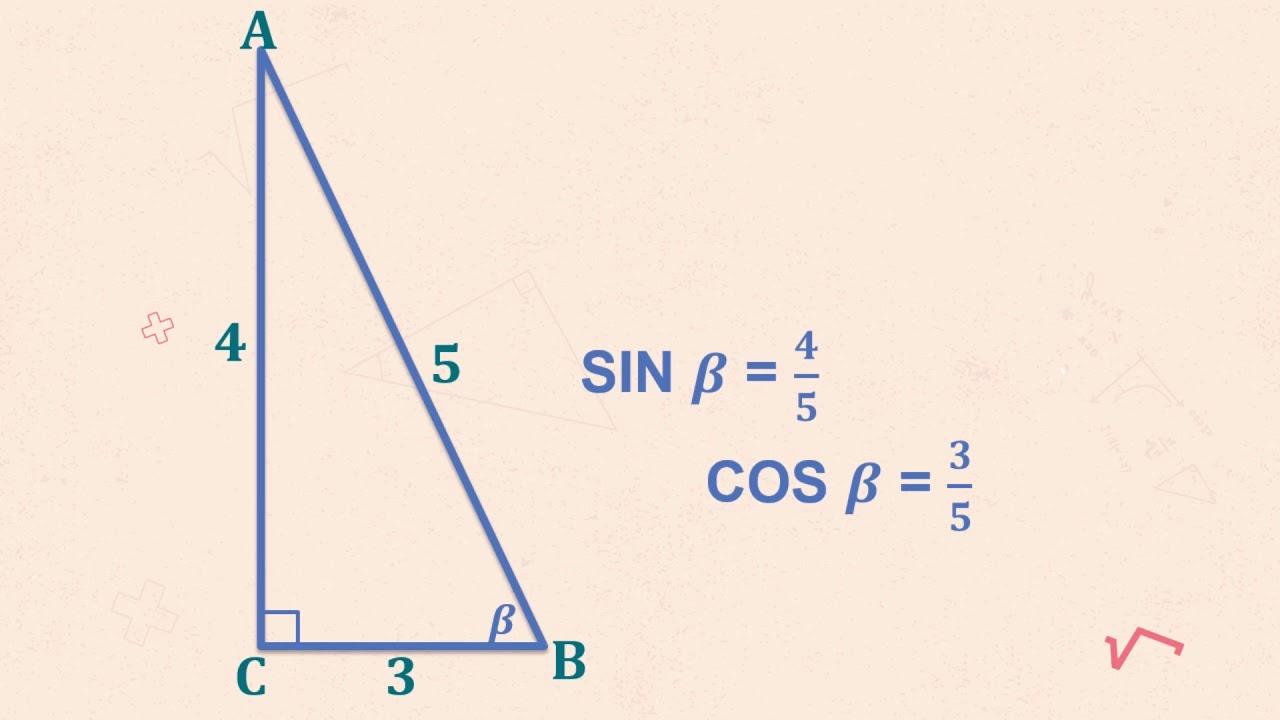
How do you identify the opposite, adjacent, and hypotenuse sides relative to an angle in a triangle?

The hypotenuse is always opposite the 90° angle. The opposite side is the one directly opposite the angle you are considering, while the adjacent side is the side next to the angle but not the hypotenuse.

What are the three basic trigonometric ratios?

The three basic trigonometric ratios are: sin (sine), cos (cosine), and tan (tangent). These ratios are defined as: sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/adjacent.

How do you remember the relationships for the trig ratios?

A helpful mnemonic for remembering the trig ratios is 'SOH-CAH-TOA'. This stands for: Sine = Opposite/Hypotenuse (SOH), Cosine = Adjacent/Hypotenuse (CAH), Tangent = Opposite/Adjacent (TOA).

What is the formula for finding sin, cos, and tan for a given angle in a triangle?

For a given angle (denoted as θ or any other label), the formulas are as follows: - sin(θ) = opposite/hypotenuse, - cos(θ) = adjacent/hypotenuse, - tan(θ) = opposite/adjacent.

How can you solve for missing sides in a right-angled triangle?

To solve for missing sides in a right-angled triangle, you can use trigonometric ratios if the angle is known, or you can use the Pythagorean theorem (a² + b² = c²) if two sides are known.

Why do we need to simplify fractions when using trigonometric ratios?

Simplifying fractions helps to express the answer in its simplest form, making it easier to interpret and use in further calculations or applications.