The Fourier Series and Fourier Transform Demystified
Summary
TLDRIn this episode of 'Up and Atom', Jade explores the fascinating world of Fourier series and transforms, revealing how they can decompose any function into sine and cosine waves. From digital music to quantum mechanics, these mathematical tools are ubiquitous. Jade demonstrates how adding waves can approximate complex shapes like square waves, and how Fourier analysis aids in pattern recognition. The video also touches on the practical applications of these concepts, such as filtering out unwanted frequencies in audio recordings.
Takeaways
- 📚 The Fourier series allows any function to be represented as a sum of sine and cosine waves, which is foundational for understanding various scientific and technological applications.
- 🌊 The concept of adding sine and cosine waves together can approximate more complex wave shapes, like square waves, by adjusting amplitude and frequency.
- 🔍 Fourier series are infinite sums, suggesting that with an infinite number of terms, any function can be exactly represented by these waves.
- 🎛️ Adjusting the amplitude of the sine and cosine components in a Fourier series can significantly alter the shape of the resulting wave, making it closer to desired forms like square or sawtooth waves.
- 🛠️ Fourier analysis is practical in real-world applications, such as pattern recognition and image analysis, where it helps in distinguishing between different shapes and patterns.
- 🎵 The Fourier transform is a powerful tool that can extract or remove specific frequencies from a function, which is useful in signal processing, like removing high-pitched sounds from audio recordings.
- 🌐 The Fourier transform provides a frequency domain view of a function, which is different from the time domain representation, offering new insights and manipulation capabilities.
- 🔄 The process of finding the Fourier series involves complex mathematical operations, including the use of Euler's Formula and integrals, to determine the correlation between the original function and sine/cosine waves.
- 📊 The Fourier transform can be visualized as changing the basis of a function from time to frequency, similar to changing the coordinate system in vector spaces.
- 🌐 Algorithms based on Fourier analysis are integral to many technologies, from video streaming to medical procedures, often working quietly behind the scenes to enhance our daily experiences.
Q & A
What is the main topic discussed in the 'Up and Atom' episode sponsored by Curiosity Stream?
-The main topic discussed is the Fourier series and its application in various fields such as digital music, quantum mechanics, and image recognition.
How does the Fourier series represent any function?
-The Fourier series represents any function by summing up an infinite series of sine and cosine waves, which can approximate the shape of any function, even those with sharp corners like a square wave.
What is the significance of adding sine and cosine waves of different frequencies and amplitudes?
-Adding sine and cosine waves of different frequencies and amplitudes allows for the approximation of more complex waveforms, such as square waves and sawtooth waves, which are essential in signal processing and pattern recognition.
Why is the Fourier series useful even if it involves dealing with infinite sums?
-The Fourier series is useful because it allows us to represent complex functions in terms of simpler sine and cosine functions, which can be easier to analyze and manipulate. In practice, we often only need an approximation that is good enough for the application at hand, rather than a perfect solution.
How does the Fourier series relate to pattern and shape recognition?
-The Fourier series can be used to analyze the outlines of objects, such as distinguishing between an apple and a slice of pizza, by breaking down their shapes into a series of sine and cosine waves, which can then be used for identification.
What is the role of the Fourier transform in the context of the Fourier series?
-The Fourier transform is a tool that can be used to pick out which frequencies or sines and cosines are present in a function, without needing to find the Fourier series explicitly. It can also be used to remove specific frequencies from a function, such as eliminating a high-pitched sound from a recording.
How does the Fourier transform provide a frequency domain view of a time domain function?
-The Fourier transform decomposes a function into its constituent sine and cosine waves, focusing on the amplitude and frequency of these waves. It provides a frequency domain view by representing the function in terms of amplitudes at various frequency values, rather than at specific time positions.
What is Euler's Formula, and how does it relate to the Fourier transform?
-Euler's Formula states that a complex exponential can be written in terms of sine and cosine waves. This formula is crucial to the Fourier transform because it allows the transformation of a time function into its frequency components by using the exponential term in the Fourier transform equation.
How does the process of multiplying the time function by an exponential term and taking the integral help in determining the Fourier series?
-Multiplying the time function by an exponential term and taking the integral helps in determining the Fourier series by calculating the correlation between the original function and the sine and cosine waves at various frequencies. The integral of these products gives the amplitude of each frequency component in the Fourier series.
Why are only odd sine terms present in the Fourier series of a square wave?
-Only odd sine terms are present in the Fourier series of a square wave because each period of the square wave has more correlation humps than anti-correlation humps, leading to a positive sum. Even frequencies and cosine waves would result in a sum of zero, as the positive and negative humps cancel each other out.
What is the significance of the orthogonal basis in the context of the Fourier series and Fourier transform?
-The orthogonal basis, consisting of sine and cosine waves, is significant because it allows for the combination of these waves to represent any function in function space, similar to how an orthogonal vector basis can represent any vector in a vector space. This property is essential for the Fourier series and transform to work effectively in changing the basis of functions.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
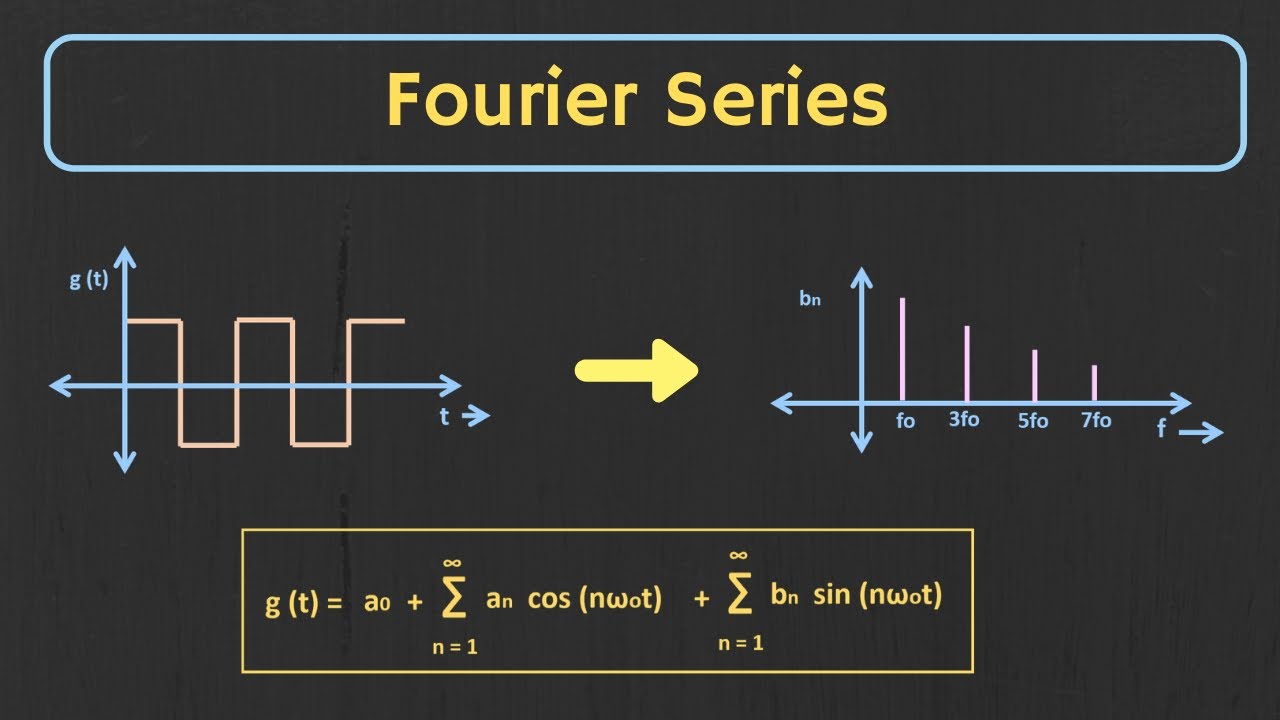
Introduction to Fourier Series | Trigonometric Fourier Series Explained
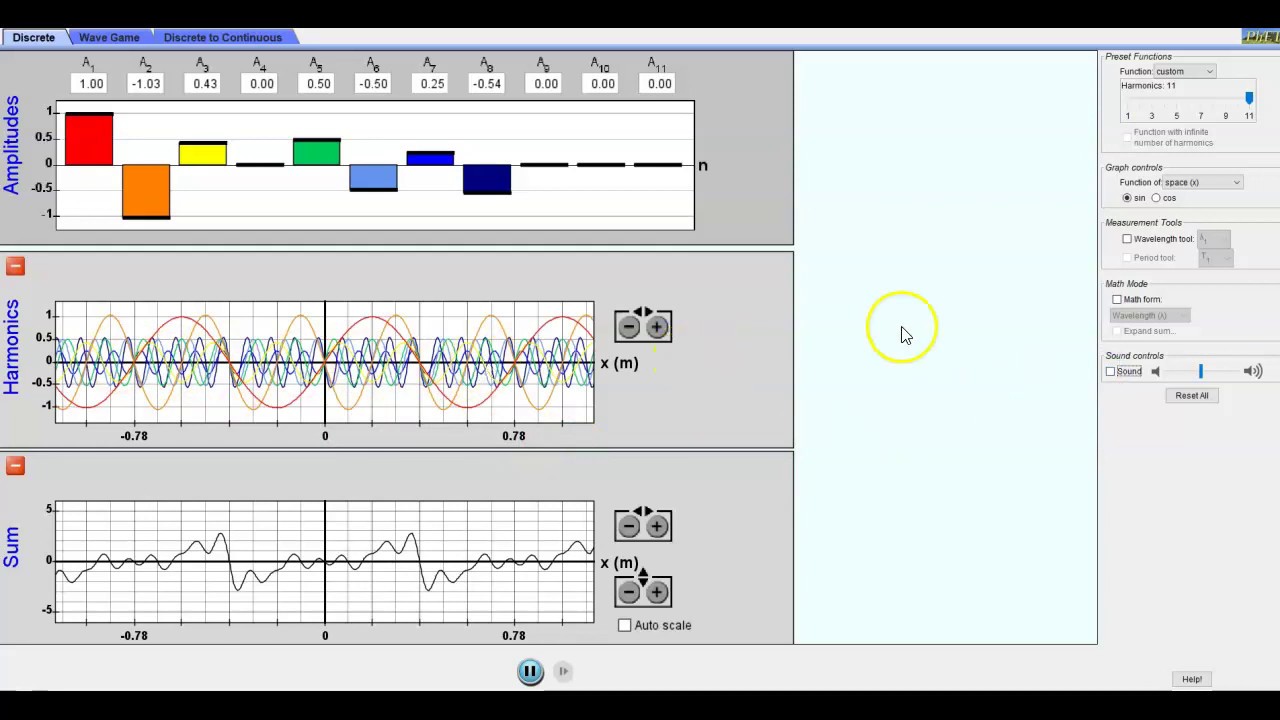
Introduction to PhET Fourier: Making Waves Simulation

But what is a Fourier series? From heat flow to drawing with circles | DE4

I Prodigi della TRASFORMATA di FOURIER
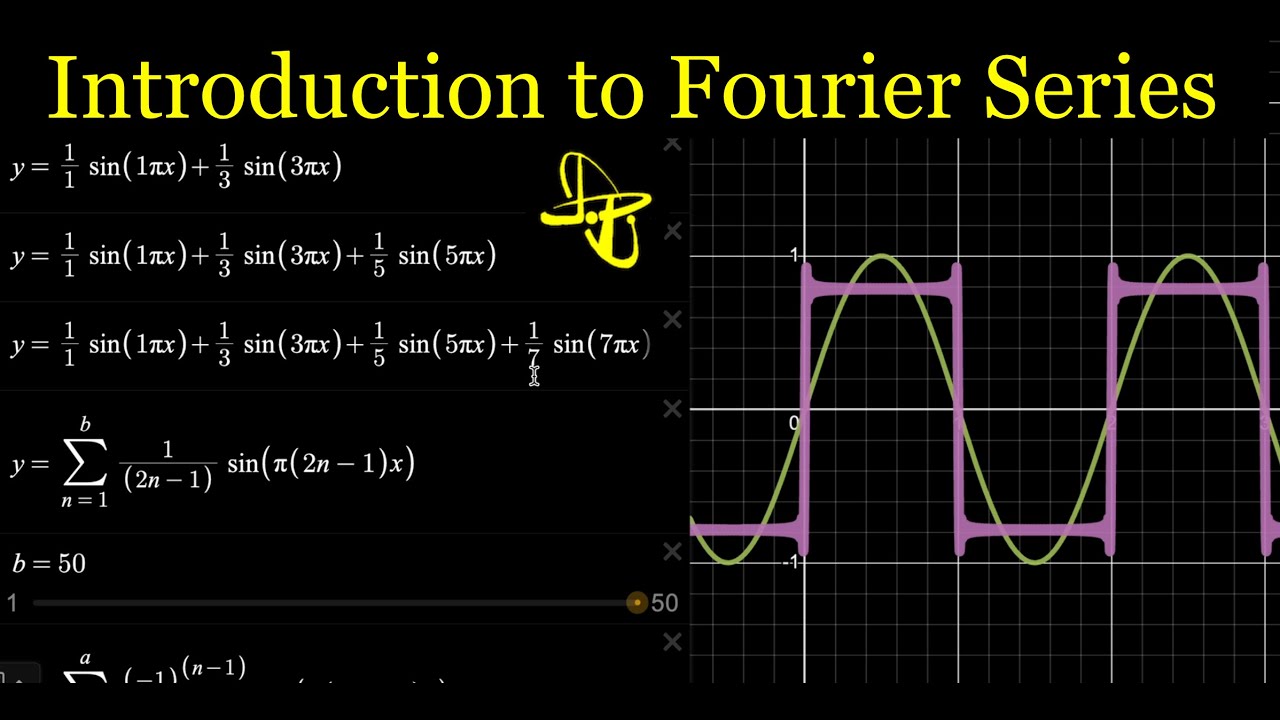
Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves
Sine Wave | Simple Explanation on a Giant or Ferris Wheel | Trigonometry | Learnability
5.0 / 5 (0 votes)
