Introduction to PhET Fourier: Making Waves Simulation
Summary
TLDRThis video introduces the Fourier Transform using an interactive simulation that demonstrates the creation of various waveforms, including sine, cosine, triangle, square, and sawtooth waves. The process highlights how individual wave components combine to form complex shapes, focusing on concepts like symmetry, amplitude, and frequency. It emphasizes the connection between Fourier Transforms and sound synthesis, helping viewers understand how different waveforms relate to quantum mechanics and physics. The video also includes a hands-on game to deepen conceptual understanding of how these waves function, making it a valuable learning tool.
Takeaways
- 😀 Fourier transforms break complex waveforms into simpler sinusoidal components, such as sine and cosine waves.
- 😀 The coefficients (a1 to a11) represent different terms of the sum, and each term contributes to the overall shape of the waveform.
- 😀 The transition from sine to cosine changes the symmetry of the wave, with sine starting at zero and cosine starting at its peak.
- 😀 The key aspect of a waveform is its periodicity, where the shape repeats consistently across time or space.
- 😀 You can modify the amplitude and direction of the waves, changing their appearance while maintaining periodicity.
- 😀 The program demonstrates how varying the number of terms in a wave approximation impacts its appearance, such as with square waves requiring many terms for sharp edges.
- 😀 The simulation allows users to visually see how different waveforms (triangle, square, sawtooth) can be approximated by summing sine and cosine terms.
- 😀 Higher frequency terms are needed to create sharper edges in waveforms like square waves, reflecting how energy and wavelength are linked.
- 😀 Wave packets are Gaussian-shaped distributions that are commonly used in quantum mechanics, though the simulation is simplified for sound and general wave analysis.
- 😀 The game feature in the simulation helps users learn Fourier transforms by matching waveforms with their corresponding coefficient sums.
- 😀 Time and space are interchangeable in this simulation, depending on whether you’re studying sound or wave mechanics in quantum contexts.
Q & A
What is the purpose of the Fourier Transform in this simulation?
-The Fourier Transform is used to break down complex waveforms into simpler sinusoidal components, allowing for the analysis of different frequencies and amplitudes that make up the waveform.
Why do all the sine waves start at zero and go up initially?
-All sine waves start at zero and go up because they are periodic functions, and sine waves specifically begin at zero due to their mathematical properties, where the sine of zero is zero.
What happens when the amplitude of a sine wave is made negative in the simulation?
-When the amplitude is made negative, the sine wave starts at zero but goes down initially, flipping the wave along the horizontal axis, creating an inverted version of the original wave.
What does the period of a sine wave refer to, and how is it related to space in this context?
-The period of a sine wave refers to the distance over which the wave repeats itself. In this context, it's referred to as space, indicating how the wave function behaves over a specific distance.
What is the significance of the symmetry of waveforms in this simulation?
-The symmetry of waveforms, such as sine and cosine waves, plays a key role in their behavior. For instance, the reflection symmetry of cosine waves differs from the symmetry of sine waves, which affects how the wave is represented and manipulated in the simulation.
How does the simulation differentiate between space and time in waveforms?
-In the simulation, space refers to the spatial aspect of the wave, while time refers to the temporal aspect. By switching the axis from space (X) to time (T), the behavior of the wave is viewed in a different context, affecting its frequency representation.
What is the role of harmonics when approximating complex waveforms like square waves?
-Harmonics are higher-frequency components that, when added together, can approximate complex waveforms like square waves. More harmonics are required to make the edges of the square wave sharper, illustrating how higher frequencies correlate with sharper features.
What does the simulation reveal about the relationship between energy and waveform sharpness?
-The simulation shows that sharper features in waveforms, such as square or sawtooth waves, require higher energy, which corresponds to higher-frequency components and smaller wavelengths. This demonstrates the connection between waveform sharpness and the need for higher harmonics.
How do different waveforms like triangle waves and sawtooth waves behave in the simulation?
-Triangle waves exhibit a pattern of high and low magnitudes that gradually diminish, while sawtooth waves continuously add terms without skipping, showing different symmetry and requiring additional terms to sharpen their edges.
How does the wave game in the simulation help users understand the Fourier Transform?
-The wave game challenges users to match a target waveform by adjusting the frequencies and amplitudes of individual components. This hands-on experience helps users intuitively grasp how the Fourier Transform works by thinking through how different frequencies combine to form complex waveforms.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
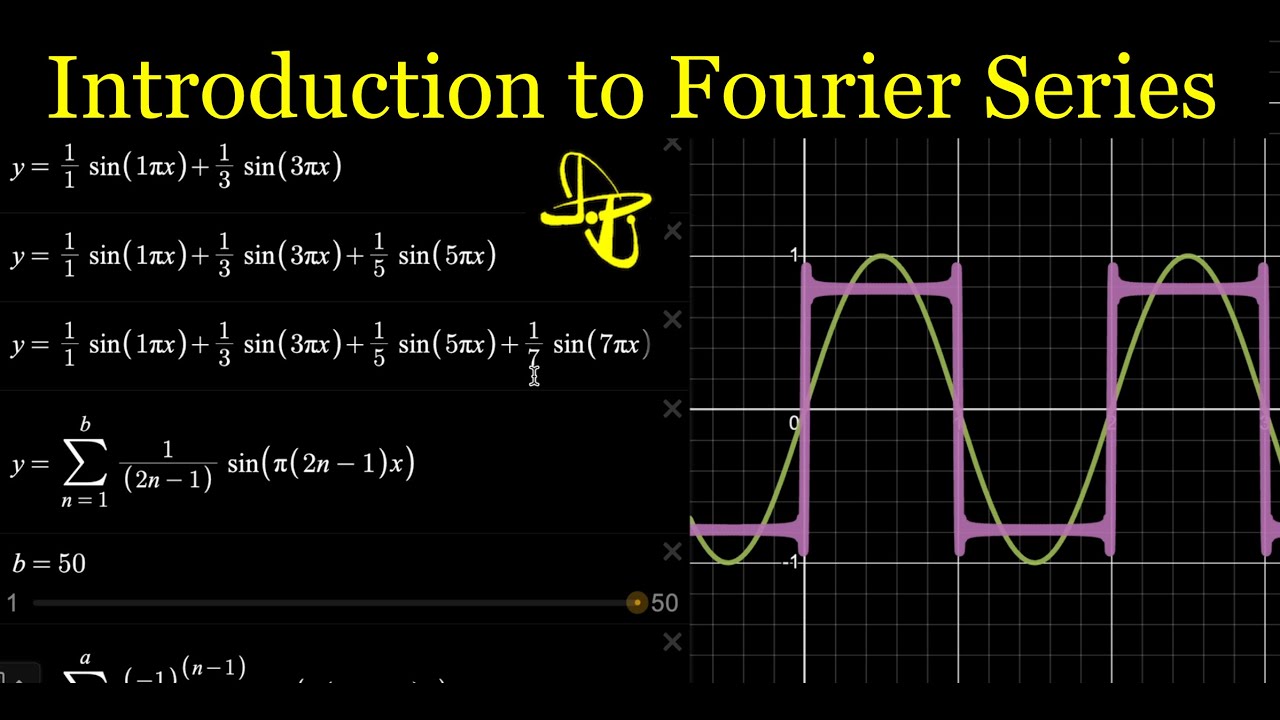
Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves

I Prodigi della TRASFORMATA di FOURIER

The Fourier Series and Fourier Transform Demystified

Sound Design and Synth Fundamentals

The Fourier Transform and Endoscopic Ultrasounds | Trisha Boonpongmanee | TEDxDeerfield
MRI Physics Fourier Transform for MRI Kucharczyk
5.0 / 5 (0 votes)