Düzgün Çembersel Hareket - 1 | Temel Kavramlar | PDF
Summary
TLDRThe transcript discusses the principles of rotational motion, focusing on concepts such as angular velocity, period, and frequency. It illustrates how different points on a rotating object experience the same angular displacement but differ in linear speed based on their distance from the rotation axis. Using relatable examples, such as a ballerina spinning, it emphasizes the relationship between angular and linear velocities. The session concludes with a problem-solving segment, demonstrating how to calculate period and angular speed using given parameters, reinforcing the theoretical concepts through practical application.
Takeaways
- 😀 The angular displacement of rotating bodies is consistent across all points on the object regardless of their distance from the rotation axis.
- 😀 The linear velocity of points on a rotating body increases with their distance from the center of rotation.
- 😀 All points on a rigid body rotating about a fixed axis experience the same angular speed.
- 😀 The relationship between linear speed and angular speed can be expressed as linear speed = angular speed × radius.
- 😀 In circular motion, the period is the time taken to complete one full rotation, while frequency is the number of rotations per unit time.
- 😀 The circumference of a circle is calculated as 2π times the radius, which is essential for determining the distance traveled during rotation.
- 😀 When analyzing circular motion, the concept of centripetal acceleration is important for understanding the forces acting on the body.
- 😀 Examples from real life, like a ballerina's movements, illustrate how distance from the rotation center affects linear speed.
- 😀 Understanding the equations for angular velocity helps in solving problems related to rotational dynamics.
- 😀 Practical applications of circular motion concepts can be found in various fields, including engineering and physics.
Q & A
What is the relationship between angular velocity and linear velocity in circular motion?
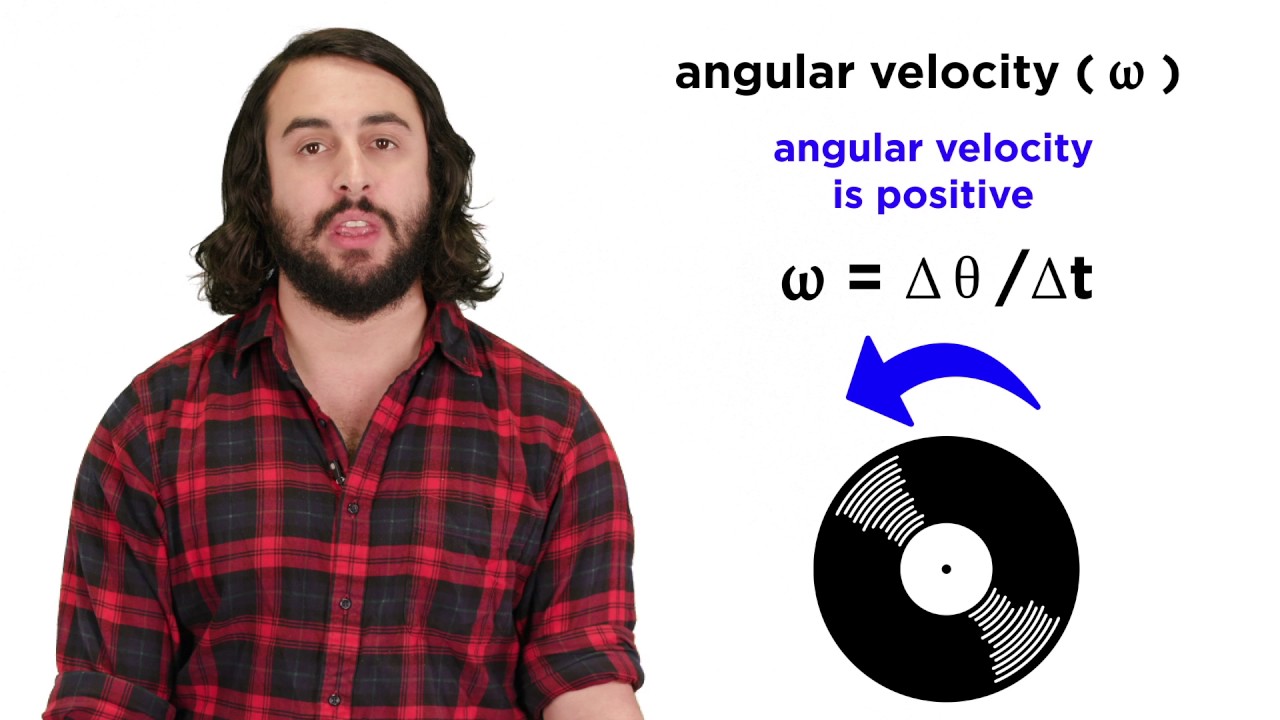
-Angular velocity is the rate of rotation of an object around a central point, while linear velocity is the speed at which a point on the object's perimeter moves. The relationship is defined by the equation: linear velocity = angular velocity × radius.
How can we determine the period of a circular motion?
-The period is the time taken for one complete revolution. It can be calculated using the formula: period = distance traveled (circumference of the circle) / speed.
What is meant by 'angular displacement' in the context of rotating objects?
-Angular displacement refers to the angle through which an object has rotated about a specific point, measured in degrees or radians.
Why do points farther from the center of rotation have higher linear speeds?
-Points farther from the center have to cover a greater distance in the same time period, resulting in a higher linear speed. This is due to the relationship between the radius and the arc length traveled.
What is the significance of the 'reference point' in rotation?
-The reference point is essential for determining the position and motion of rotating objects. It is the point around which the object rotates, and all measurements of angles and distances are taken relative to it.
How can the frequency of rotation be calculated?
-Frequency is calculated as the inverse of the period: frequency = 1 / period. It indicates how many complete rotations occur in a unit of time.
What does it mean for angular velocities to be equal for all points on a rotating object?
-This means that every point on the object rotates through the same angle in the same amount of time, ensuring a uniform rotation throughout the object.
How does the concept of centrifugal force relate to circular motion?
-Centrifugal force is an apparent force that acts outward on a mass moving in a circular path, perceived from the rotating frame of reference. It is the result of inertia, as the mass tries to move in a straight line while being constrained to circular motion.
Can you explain the difference between linear and angular acceleration?
-Linear acceleration refers to the rate of change of linear velocity, while angular acceleration refers to the rate of change of angular velocity. They are related but measure different aspects of motion.
What are some real-life applications of the concepts discussed in the script?
-Real-life applications include understanding the motion of planets, designing amusement park rides, and analyzing the motion of vehicles around curves. These principles are crucial in engineering and physics.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)