Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration
Summary
TLDRThis video provides a comprehensive overview of rotational motion, explaining key concepts such as angular position, displacement, velocity, and acceleration. It distinguishes between rotational and linear motion while introducing essential terms like period and frequency. The video emphasizes the relationship between linear and angular velocities, using relevant equations to illustrate these concepts. Additionally, it explores types of acceleration—centripetal and tangential—and how they contribute to the net acceleration of an object in circular motion. Overall, this educational resource aims to deepen understanding of the dynamics of rotating objects.
Takeaways
- 😀 Rotational motion refers to any object that rotates or spins, differing from linear motion where an object moves forward.
- 🔄 Key terms in rotational motion include angular position and angular displacement, similar to position and displacement in linear motion.
- 📐 Angular displacement is measured in radians, with degrees also being used but less commonly in scientific contexts.
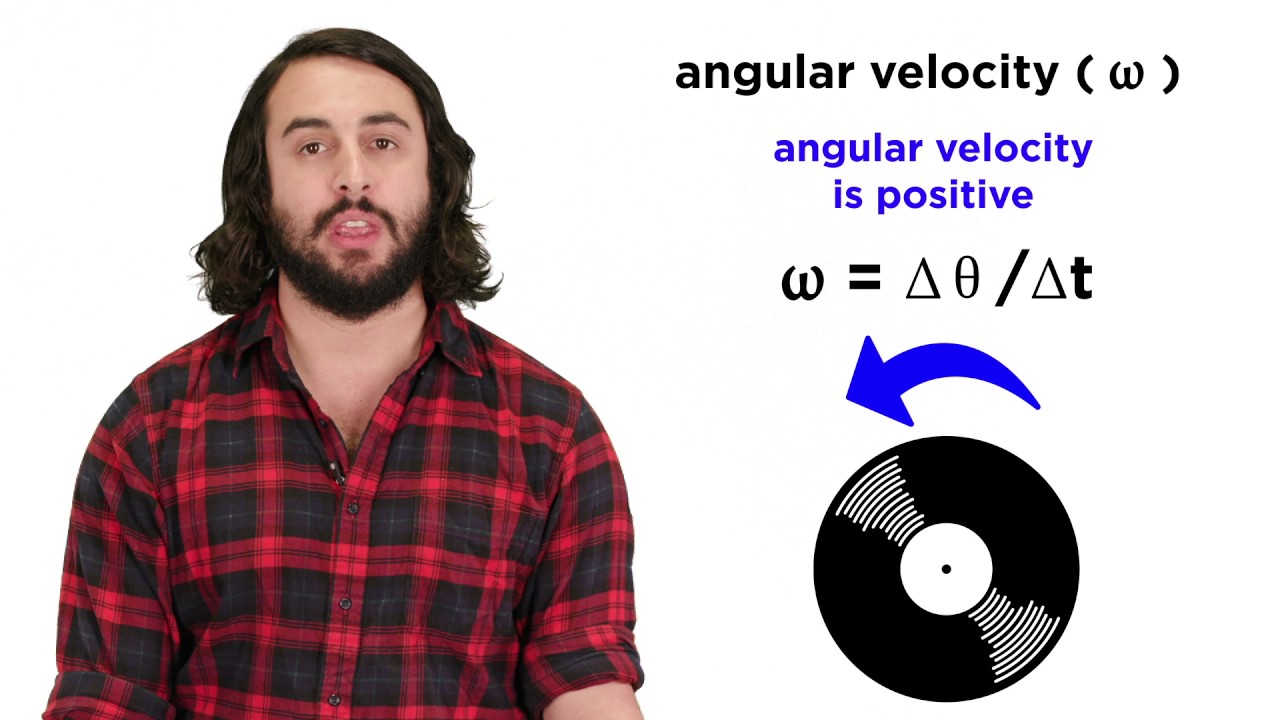
- ⏱️ Angular velocity (ω) indicates how fast an object is spinning, calculated as angular displacement divided by time.
- ⚙️ The equation connecting linear velocity (v) to angular velocity is v = ω * r, where r is the radius of the circle.
- 🌍 For an object rotating, all points have the same angular velocity, but linear velocity varies with distance from the center.
- 🔄 The period of rotation is the time taken to complete one cycle, while frequency is the number of cycles per second.
- 🧮 Angular velocity can be calculated using the frequency with the equation ω = 2πf.
- 🏎️ Linear acceleration and angular acceleration follow similar definitions, with angular acceleration being the change in angular velocity over time.
- 🌀 Centripetal acceleration points toward the center of the circle and is calculated as the linear speed squared divided by the radius.
Q & A
What is the definition of rotational motion?
-Rotational motion refers to the movement of an object that rotates or spins around an axis, distinguishing it from linear motion, where an object moves in a straight line.
How does angular position differ from linear position?
-Angular position describes a point on a circle, while linear position refers to a point on a straight number line. Both concepts indicate a specific location in their respective contexts.
What is angular displacement and how is it calculated?
-Angular displacement is the difference between the final angular position and the initial angular position, represented as Δθ. It is measured in radians.
What are the units for angular velocity and how is it defined?
-Angular velocity, denoted as ω, measures how fast an object spins around a circle and is defined as the change in angular displacement over time, with units of radians per second.
How is linear velocity related to angular velocity?
-Linear velocity (v) is related to angular velocity (ω) by the equation v = ω × r, where r is the radius of the circular path.
What is the difference between period and frequency in rotational motion?
-The period (T) is the time taken to complete one full cycle or rotation, while frequency (f) is the number of cycles that occur per second. They are related by the equation f = 1/T.
What are the standard units for angular and linear acceleration?
-Angular acceleration is measured in radians per second squared (rad/s²), while linear acceleration is measured in meters per second squared (m/s²).
What is centripetal acceleration and how is it calculated?
-Centripetal acceleration (Ac) is directed towards the center of the circular path and is calculated using the formula Ac = v²/r or Ac = ω² × r.
What is the relationship between tangential acceleration and angular acceleration?
-Tangential acceleration (At) is related to angular acceleration (α) by the equation At = α × r, indicating that it measures the change in linear speed at a point on the rotating object.
How do centripetal and tangential accelerations combine when an object is moving in circular motion?
-When an object moves in circular motion with varying speed, the net acceleration is the vector sum of centripetal and tangential accelerations, resulting in a total acceleration vector that can be found using the Pythagorean theorem.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

PHYS 121 - Week 6 Lecture 2 - Rotational Motion

Rigid Bodies: Rotation About a Fixed Axis Dynamics (learn to solve any question)
Angular Motion and Torque

Rotational Motion

Rotational Kinematics Physics Problems, Basic Introduction, Equations & Formulas
Angular Motion | Sport Science Hub: Biomechanics Fundamentals | Updated 2021 No Music
5.0 / 5 (0 votes)