Problema 11-44 Cengel. Método LMTD.
Summary
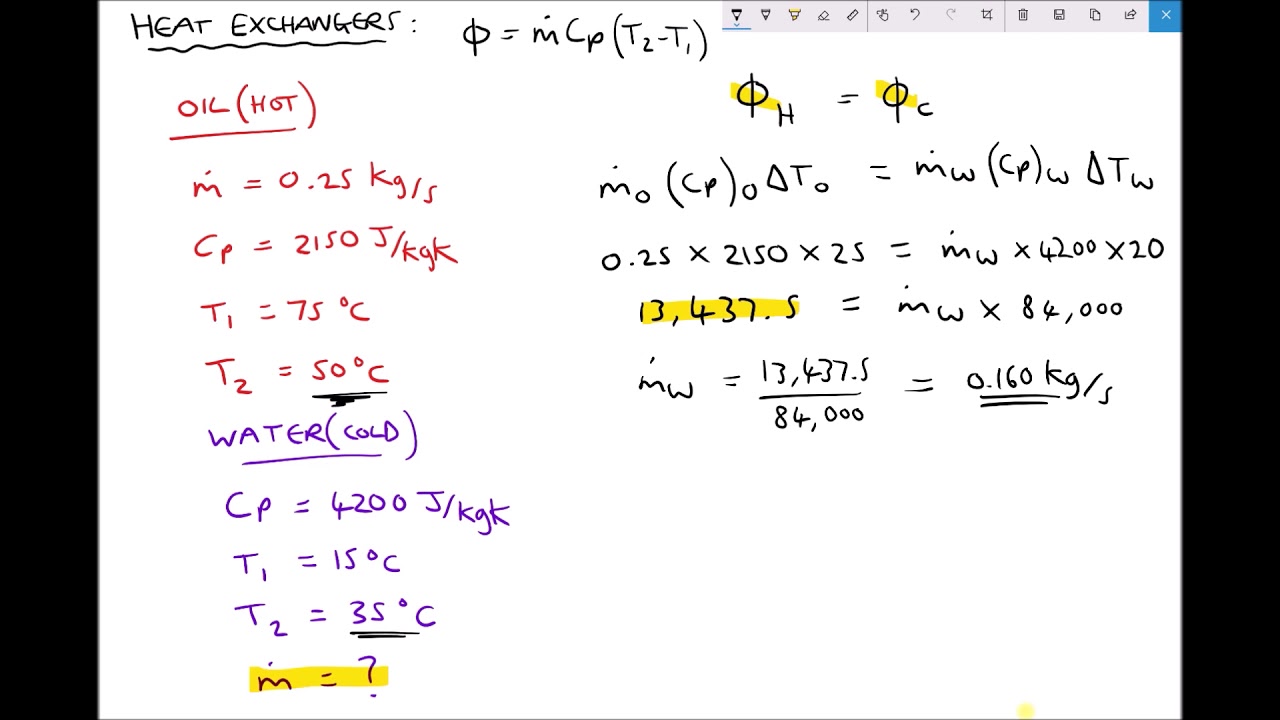
TLDRThis script demonstrates the application of the logarithmic mean temperature difference method in heat transfer calculations. It details a carbon dioxide cooling process in a double-pipe counterflow heat exchanger, where 720 kg/h of CO2 is cooled from 150°C to 40°C. The cold fluid, water, enters at 10°C and exits at a calculated temperature. The script guides through the steps of determining the heat flow, using the specific heat capacity (cp), mass flow rate, and temperature differences. It concludes with the calculation of the overall heat transfer coefficient, resulting in a value of 2311, providing a clear example of thermal engineering principles.
Takeaways
- 🔍 The script discusses a simple problem to illustrate the application of the logarithmic mean temperature difference method in heat transfer calculations.
- 🌡️ The problem involves a carbon dioxide flow being cooled from 150°C to 40°C at a rate of 720 kg/h in a double-pipe heat exchanger with counter-flow.
- 💧 Water enters the heat exchanger at 10°C at a rate of 540 kg/h and is heated by the carbon dioxide.
- 📏 The outer diameter of the inner tube is 2.5 cm, and its length is 6 meters, which are key dimensions for calculating the heat transfer area.
- ⏱️ The heat transfer rate is calculated using the mass flow rate, specific heat capacity (cp), and the temperature difference between the inlet and outlet of the hot fluid.
- 🔄 The counter-flow arrangement is important as it affects the temperature gradients and the calculation of the outlet temperature of the cold fluid.
- ⚖️ The logarithmic mean temperature difference is used to account for the varying temperature differences along the length of the heat exchanger.
- 📐 The area of the heat transfer surface is calculated by multiplying the tube's diameter by its length, which is essential for determining the overall heat transfer coefficient.
- 🔢 The overall heat transfer coefficient is determined by rearranging the heat transfer equation and solving for the coefficient, resulting in a value of 2311 in this case.
- 🔧 The problem emphasizes the importance of congruence in the calculations to ensure the accuracy of the heat transfer coefficient.
- 📝 The script provides a step-by-step approach to solving heat transfer problems using the logarithmic mean temperature difference method, which is crucial for designing and analyzing heat exchangers.
Q & A
What problem is being discussed in the script?
-The script discusses a problem involving the application of the logarithmic mean temperature difference method in a heat exchanger scenario to calculate the total heat transfer coefficient.
What is the hot fluid in this problem and what are its properties?
-The hot fluid is carbon dioxide (CO2) with a specific heat capacity (cp) of 2200 J/kg·K, an inlet temperature of 150°C, and an outlet temperature of 40°C. It flows at a rate of 720 kg/h.
What is the flow rate of the hot fluid in kg/s?
-The flow rate of the hot fluid is 720 kg/h, which is equivalent to 0.2 kg/s (720 kg/3600 s).
What is the purpose of the heat exchanger in this scenario?
-The purpose of the heat exchanger is to cool down the hot fluid (carbon dioxide) by transferring heat to the cold fluid (water) through a double-pipe counterflow heat exchanger.
What is the cold fluid in this problem and its flow rate?
-The cold fluid is water with an inlet temperature of 10°C. It flows at a rate of 540 kg/h.
What are the dimensions of the inner tube in the heat exchanger?
-The inner tube has an outer diameter of 2.5 centimeters and a length of 6 meters.
How is the total heat transfer calculated?
-The total heat transfer is calculated by multiplying the mass flow rate of the hot fluid (720 kg/h) by its specific heat capacity (2200 J/kg·K) and the temperature difference (150°C - 40°C).
What is the concept of the logarithmic mean temperature difference method?
-The logarithmic mean temperature difference (LMTD) method is a way to calculate the average temperature difference between the hot and cold fluids in a heat exchanger, which is used to determine the heat transfer rate.
How is the outlet temperature of the cold fluid determined?
-The outlet temperature of the cold fluid is determined by dividing the total heat transfer by the mass flow rate of the cold fluid (540 kg/h), its specific heat capacity, and then adding it to the inlet temperature of the cold fluid.
What is the calculated global heat transfer coefficient?
-The calculated global heat transfer coefficient is 2311 W/m²·K, which represents the overall efficiency of heat transfer in the heat exchanger.
Why is it important to calculate the surface area of the tube?
-Calculating the surface area of the tube is important because it is used in conjunction with the LMTD to determine the overall heat transfer coefficient, which is a key parameter in the design and analysis of heat exchangers.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Heat Transfer (27) - Heat transfer in internal flows in tubes
Calculating Rate of Heat Transfer Between Two Working Fluids of a Heat Exchanger

GCSE Physics - Internal Energy and Specific Heat Capacity #28

Thermal energy, temperature, and heat | Khan Academy

Física - Calor Sensível e Calor Latente

Heat Transfer - Chapter 8 - Internal Convection - Hydrodynamic Considerations
5.0 / 5 (0 votes)
