Suma y diferencia de ángulos: problemas de trigonometría
Summary
TLDREn este video tutorial, el profesor explica cómo calcular la suma y diferencia de ángulos en trigonometría. Se presentan seis fórmulas clave para sumar o restar seno, coseno y tangente de ángulos, y cómo dependen del signo. Se utiliza el ejemplo práctico de calcular el seno, coseno y tangente de 15 grados a partir de los ángulos de 45 y 30 grados. El profesor guía paso a paso a través de las ecuaciones, destacando la importancia de aplicar las fórmulas correctamente y el cuidado con los signos. Además, ofrece recursos adicionales para práctica adicional.
Takeaways
- 📚 Se discuten las fórmulas para la suma y diferencia de ángulos en trigonometría.
- 🔢 Se presentan seis fórmulas para el seno, coseno y tangente de ángulos sumados o restados.
- ➡️ Se explica cómo cambiar el signo en las fórmulas dependiendo de la suma o resta de ángulos.
- 📐 Se utilizan las fórmulas para calcular el seno, coseno y tangente de 15 grados a partir de los ángulos 45 y 30 grados.
- 🧮 Se muestran los cálculos paso a paso para llegar a las soluciones numéricas.
- 📉 Se resalta la importancia de aplicar correctamente las fórmulas y prestar atención a los signos.
- 📝 Se sugiere que el conocimiento de estas fórmulas es fundamental para resolver problemas de trigonometría.
- 📊 Se menciona que los ángulos 45 y 30 grados son comunes en problemas de trigonometría y se utilizan para encontrar otros ángulos.
- 📖 Se ofrecen ejercicios con soluciones para practicar los conceptos aprendidos.
- 💬 Se invita a los espectadores a comentar dudas o aportar comentarios en la página web del video.
Q & A
¿Cuáles son las fórmulas para la suma y diferencia de seno, coseno y tangente de ángulos según el guion?
-Las fórmulas para la suma y diferencia de ángulos son: seno(a ± b) = seno(a)coseno(b) ± coseno(a)seno(b), coseno(a ± b) = coseno(a)coseno(b) ∓ seno(a)seno(b), y tangente(a ± b) = (tangente(a) ± tangente(b)) / (1 ∓ tangente(a)tangente(b)).
¿Cómo se determina el signo en las fórmulas de suma y diferencia de ángulos?
-El signo en las fórmulas de suma y diferencia de ángulos se determina según el tipo de operación (suma o resta) y el ángulo que se está calculando. Por ejemplo, en la fórmula de seno(a ± b), se utiliza '+' si es una suma y '-' si es una resta.
¿Qué significa el 'verde' mencionado en el guion al explicar las fórmulas de trigonometría?
-El 'verde' se refiere a los términos que se deben mantener iguales en las fórmulas de suma y diferencia de ángulos, como seno(a) y seno(b), o coseno(a) y coseno(b), para aplicar correctamente las fórmulas.
¿Cómo se calcula el seno de 15 grados utilizando las fórmulas de suma y diferencia de ángulos?
-Para calcular el seno de 15 grados, se utiliza la fórmula de resta de ángulos: seno(45 - 30) = seno(45)coseno(30) - coseno(45)seno(30), lo que da como resultado (√2/2)(√3/2) - (√2/2)(1/2), que simplifica a (√6 - √2)/4.
¿Cuál es el resultado numérico aproximado del seno de 15 grados según el guion?
-El resultado numérico aproximado del seno de 15 grados, según el guion, es (√6 - √2)/4, que se puede calcular con una calculadora para obtener un valor decimal.
¿Cómo se calcula el coseno de 15 grados utilizando las fórmulas del guion?
-El coseno de 15 grados se calcula con la fórmula de resta de ángulos: coseno(45 - 30) = coseno(45)coseno(30) + seno(45)seno(30), lo que resulta en (√2/2)(√3/2) + (√2/2)(1/2), que simplifica a (√6 + √2)/4.
¿Cuál es el resultado numérico aproximado del coseno de 15 grados según el guion?
-El resultado numérico aproximado del coseno de 15 grados, según el guion, es (√6 + √2)/4, que se puede obtener con una calculadora para obtener un valor decimal.
¿Cómo se calcula la tangente de 15 grados según el guion?
-La tangente de 15 grados se calcula con la fórmula de resta de ángulos: tangente(45 - 30) = (tangente(45) - tangente(30)) / (1 + tangente(45)tangente(30)), lo que resulta en (1 - √3/3) / (1 + 1*√3/3), que simplifica a 2 - √3.
¿Cuál es el resultado numérico aproximado de la tangente de 15 grados según el guion?
-El resultado numérico aproximado de la tangente de 15 grados, según el guion, es 2 - √3, que se puede calcular con una calculadora para obtener un valor decimal.
¿Cómo se pueden aplicar estas fórmulas para resolver problemas de trigonometría con ángulos diferentes?
-Estas fórmulas se pueden aplicar a problemas de trigonometría con ángulos diferentes cambiando los valores de a y b en las fórmulas para encontrar los seno, coseno y tangente de los ángulos resultantes.
¿Dónde pueden encontrarse ejercicios con soluciones para practicar más sobre la suma y diferencia de ángulos según el guion?
-Los ejercicios con soluciones para practicar más sobre la suma y diferencia de ángulos se pueden encontrar debajo del vídeo en la página web del profesor puntocom.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

✅ÁNGULOS COMPLEMENTARIOS Y SUPLEMENTARIOS| SUPER FÁCIL 💯| TRIGONOMETRÍA

Ángulo trigonométrico || Trigonometría 4to de Secundaria || Cap. 1

Identidades trigonométricas de suma de ángulos | Seno y Coseno de 75° sin calculadora

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera

Ángulos I - Operaciones con las medidas de ángulos y bisectriz de un ángulo - Geometría
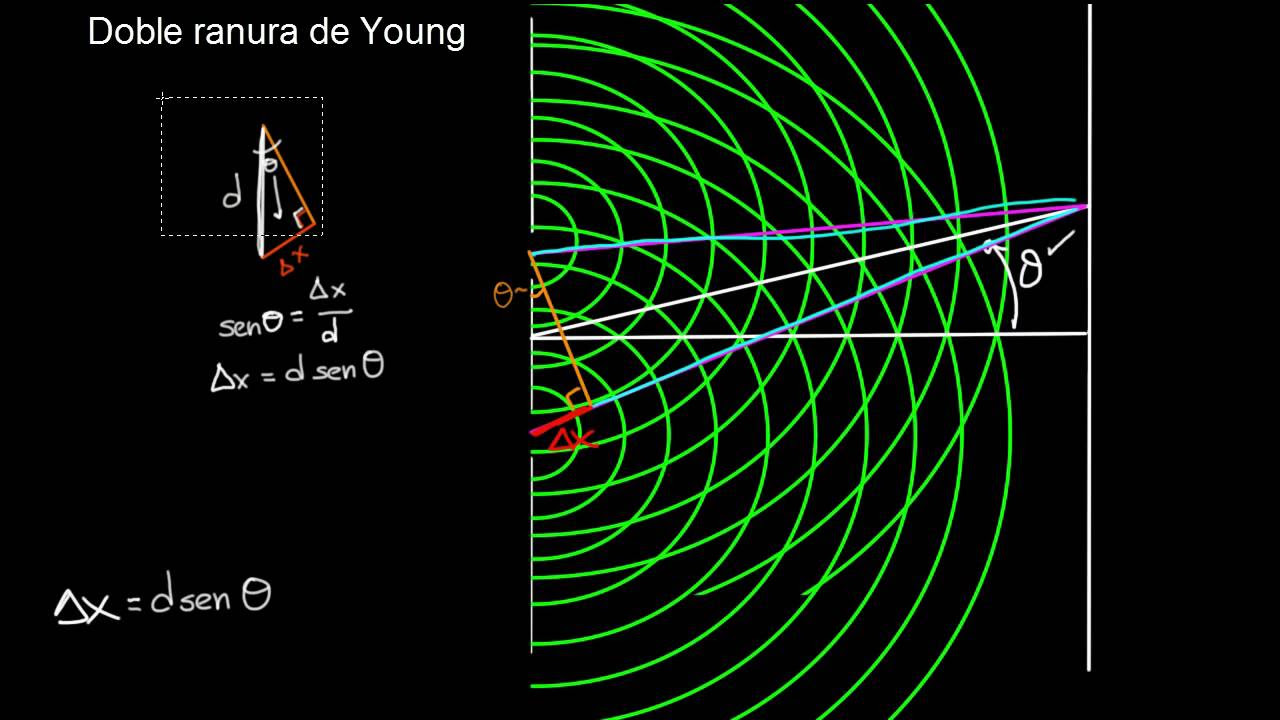
Doble ranura de Young. Parte 2 | Ondas de luz | Física | Khan Academy en Español
5.0 / 5 (0 votes)
