Criterio de la primera derivada.
Summary
TLDREn este video tutorial, el profesor Rodríguez imparte un clase de cálculo diferencial centrado en el Criterio de la Primera Derivada. Utiliza el ejemplo \( \frac{1}{3}x^3 - 4x \) para demostrar cómo encontrar valores críticos. Explicó paso a paso cómo simplificar la primera derivada, factorizarla y encontrar los puntos donde la función cambia de creciente a decreciente o viceversa. Luego, identificó los valores críticos (-2 y 2) y calculó los puntos críticos sustituyendo estos valores en la función original, obteniendo (-2, -16/3) y (2, -16/3). El video es una excelente herramienta para comprender conceptos fundamentales de cálculo.
Takeaways
- 👨🏫 El profesor Rodríguez imparte una clase de cálculo diferencial.
- 📘 Se estudia el criterio de la primera derivada para determinar los valores críticos.
- 🔍 Se utiliza el ejemplo f(x) = \( \frac{1}{3}x^3 - 4x \) para aplicar el criterio.
- ✏️ Se calcula la primera derivada f'(x) = \( x^2 - 4 \) y se factoriza para simplificar.
- 🔢 Se encuentran los valores críticos \( x = -2 \) y \( x = 2 \) al igualar la primera derivada a cero.
- 📊 Se evalúa la primera derivada en puntos que no son críticos para determinar los intervalos de crecimiento y decrecimiento.
- ↗️ La función crece en los intervalos \( (-\infty, -2) \) y \( (2, \infty) \).
- ↘️ La función decrece en el intervalo \( (-2, 2) \).
- 📌 Se identifican los puntos críticos sustituyendo los valores críticos en la función original.
- 📝 Se calculan los puntos críticos: \( f(-2) = \frac{16}{3} \) y \( f(2) = -\frac{16}{3} \).
- 🔚 El profesor Rodríguez concluye la clase y anima a suscriptores para recibir futuros tutoriales.
Q & A
¿Qué tema se aborda en la clase de cálculo diferencial impartida por el profesor Rodríguez?
-El tema tratado en la clase es el criterio de la primera derivada.
¿Cuál es la función que se utiliza como ejemplo para aplicar el criterio de la primera derivada?
-La función utilizada como ejemplo es \( f(x) = \frac{1}{3}x^3 - 4x \).
¿Cómo se calcula la primera derivada de la función dada en el ejemplo?
-La primera derivada se calcula como \( f'(x) = x^2 - 4 \).
¿Cuál es la segunda derivada de la función dada?
-La segunda derivada es \( f''(x) = 2x \).
¿Cómo se factoriza la primera derivada para encontrar los valores críticos?
-La primera derivada se factoriza como \( f'(x) = (x + 2)(x - 2) \).
¿Cuáles son los valores críticos que se obtienen al igualar la primera derivada a cero?
-Los valores críticos son \( x = -2 \) y \( x = 2 \).
¿Cómo se evalúa si los valores críticos son de crecimiento o decrecimiento de la función?
-Se evalúa sustituyendo valores en la primera derivada que no sean críticos y observando si es positiva (crecimiento) o negativa (decrecimiento).
¿Cuál es la interpretación de los valores críticos en el contexto de la función dada?
-Los valores críticos son puntos donde la función cambia de ser creciente a decreciente o viceversa.
¿Cómo se encuentran los puntos críticos en la función original?
-Se sustituye el valor crítico en la función original para encontrar el valor de y correspondiente.
¿Cuáles son los puntos críticos que se encuentran al aplicar el criterio de la primera derivada a la función dada?
-Los puntos críticos son \( (-2, \frac{16}{3}) \) y \( (2, -\frac{16}{3}) \).
¿Cómo se puede contactar al profesor Rodríguez para enviar ejercicios para ser resueltos en tutoriales futuros?
-Se puede contactar al profesor Rodríguez a través de WhatsApp o enviando un correo electrónico al que aparece en la pantalla o en la descripción del video.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

QUÉ ES EL CÁLCULO DIFERENCIAL. Explicación Básica.

Aplicaciones de la derivada a la Economía (Primera parte)
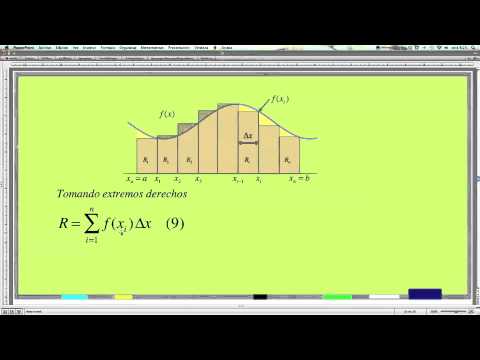
Calculo Integral 04: La integral definida. The definite integral.
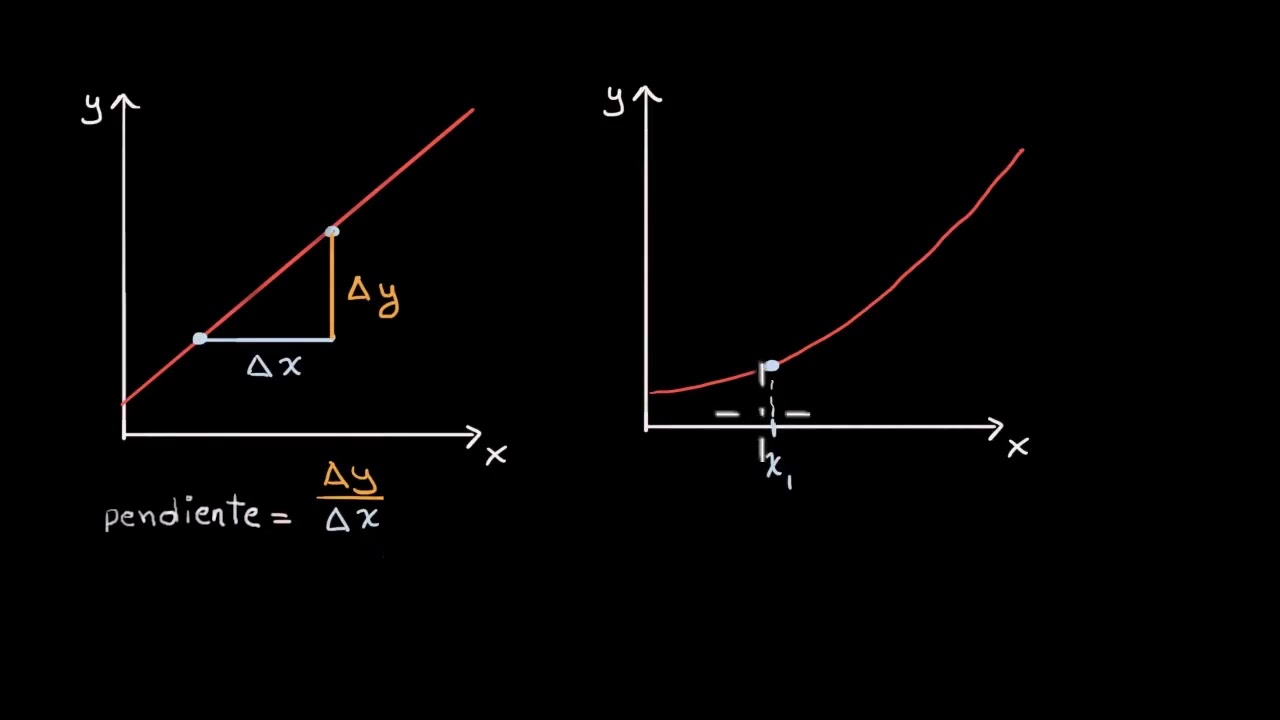
El concepto de derivada | Khan Academy en Español

Derivadas (Universo Mecánico 3)

DERIVADA DE UNA FUNCIÓN USANDO LA DEFINICIÓN - Ejercicio 2
5.0 / 5 (0 votes)
