INTEGRAL LIPAT 2 #KALKULUS 2

Summary

This video explains the concept of double integrals, also known as 'integral lipat dua,' which is an extension of single integrals where integration is performed twice. The script walks through the process of solving double integrals, both indefinite and definite, with clear explanations of each step. It includes methods like substitution, partial integration, and trigonometric substitution. The video provides a detailed example, demonstrating how to compute a specific double integral with given bounds. The visual aids in the video help clarify the process, making it easier for viewers to understand the principles behind double integrals.

Takeaways

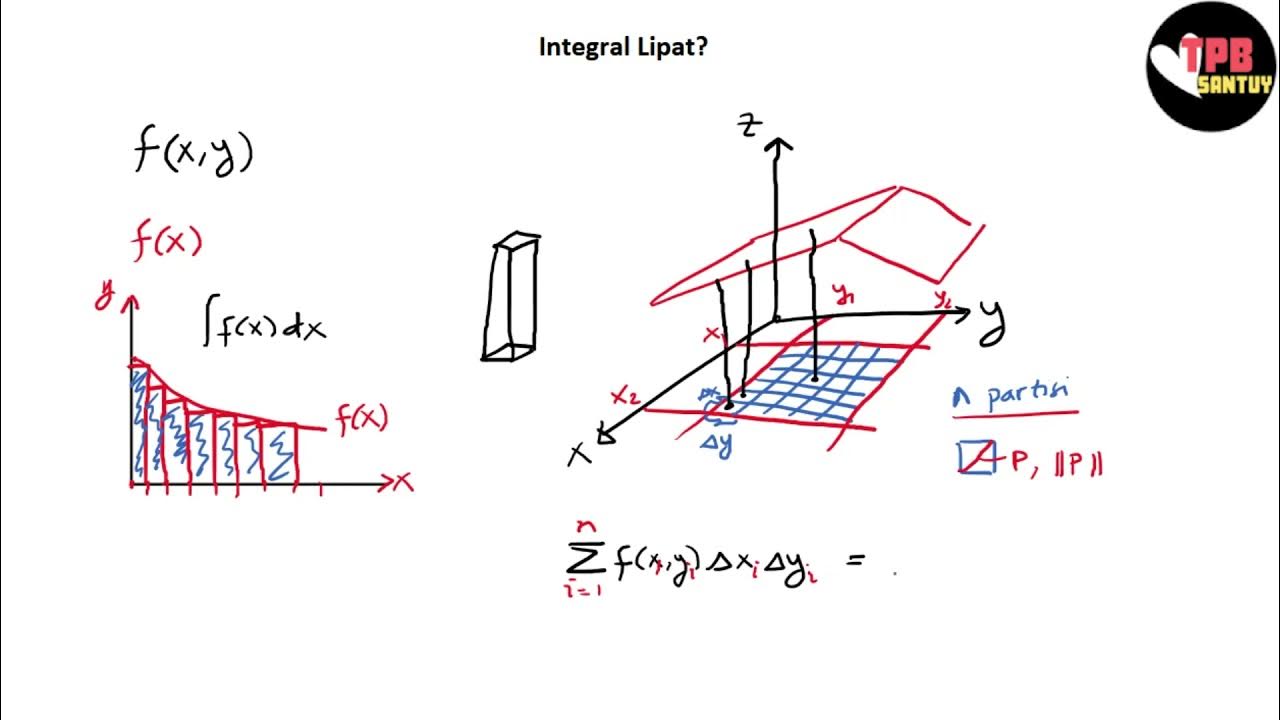
• 😀 Double integrals (integral lipat dua) are an extension of single integrals, where the result is integrated again.
• 😀 The general form of a double integral is expressed as ∫∫ f(x, y) dx dy, with limits for both variables x and y.
• 😀 Double integrals can be definite or indefinite, where definite integrals have upper and lower bounds for the variables.
• 😀 The process for solving double integrals involves integrating first with respect to one variable (e.g., x) while holding the other variable (e.g., y) constant.
• 😀 The second step in solving double integrals involves integrating with respect to the remaining variable (e.g., y), considering the first variable (e.g., x) as constant.
• 😀 In double integrals, the order of integration is crucial and typically follows the pattern of integrating the inner integral first.
• 😀 The solution involves applying basic integration techniques like substitution, partial fractions, and trigonometric substitution.
• 😀 An example is given where the integral of a function (2x - 3y) dx dy is solved step by step with specific limits for x and y.
• 😀 For definite integrals, the boundaries of integration are substituted at each stage to get the final value of the integral.
• 😀 The final result of the example calculation is 1, demonstrating how to calculate the value after integrating both variables.
• 😀 The tutorial concludes with a reminder that solving double integrals requires understanding both the process of integration and the application of boundary conditions.

Q & A

What is a double integral (integral lipat 2)?

A double integral is an extension of the single integral, where the result of one integration is integrated again. It is typically represented by the expression of an integral of a function f(x, y) with respect to x and y.

How is a double integral with specific bounds represented?

A double integral with specific bounds is represented as the integral from X1 to X2 for the variable x, and from Y1 to Y2 for the variable y. This is called a definite double integral, where each integral has its own upper and lower bounds.

What are the key principles for solving double integrals?

The key principles for solving double integrals are similar to those used in single integrals: substitution, partial integration, trigonometric substitution, and handling fractional integrals.

What is the process for solving double integrals in general?

The process for solving double integrals involves first integrating the function with respect to one variable (usually x) while treating the other variable (y) as constant, and then integrating the result with respect to the second variable (y).

How can we visualize the process of solving a double integral?

The process of solving a double integral can be visualized as two areas: the yellow area represents the first integration (with respect to x), and the green area represents the second integration (with respect to y).

How do you solve a definite double integral with specific bounds?

To solve a definite double integral, you first integrate with respect to x, substituting the upper and lower limits for x. Then, you integrate the resulting expression with respect to y, applying the limits for y.

What is the procedure for solving a double integral with bounds from 0 to 2 for x and 0 to 1 for y?

To solve this, you first integrate with respect to x, applying the bounds of 0 and 2, and then integrate the resulting expression with respect to y, applying the bounds of 0 and 1.

What is the result of integrating the function 2x - 3y with respect to x?

When integrating the function 2x - 3y with respect to x, you get the expression x^2 - 3xy, with a constant term added during the integration process.

How do you handle constants in double integrals?

Constants are treated as fixed values during integration. When integrating with respect to one variable, the constants related to the other variable are kept constant.

What does the result '4 - 3 = 1' represent in the example?

The result '4 - 3 = 1' represents the final outcome of evaluating the double integral after performing the integration steps. It comes from the process of applying the limits to the integral.