Integral lipat 2 pada daerah bukan persegi panjang

Summary

This video explains how to calculate double integrals over non-rectangular regions, with a focus on triangular areas. The speaker demonstrates how to define integration limits using geometric concepts, particularly the equation of boundary lines. By setting up the correct integration bounds, viewers learn how to calculate the integral step by step. The method applies to various shapes, not just rectangles, and emphasizes the importance of accurately determining the boundaries for proper integration. This step-by-step approach is ideal for those looking to understand double integrals in complex regions.

Takeaways

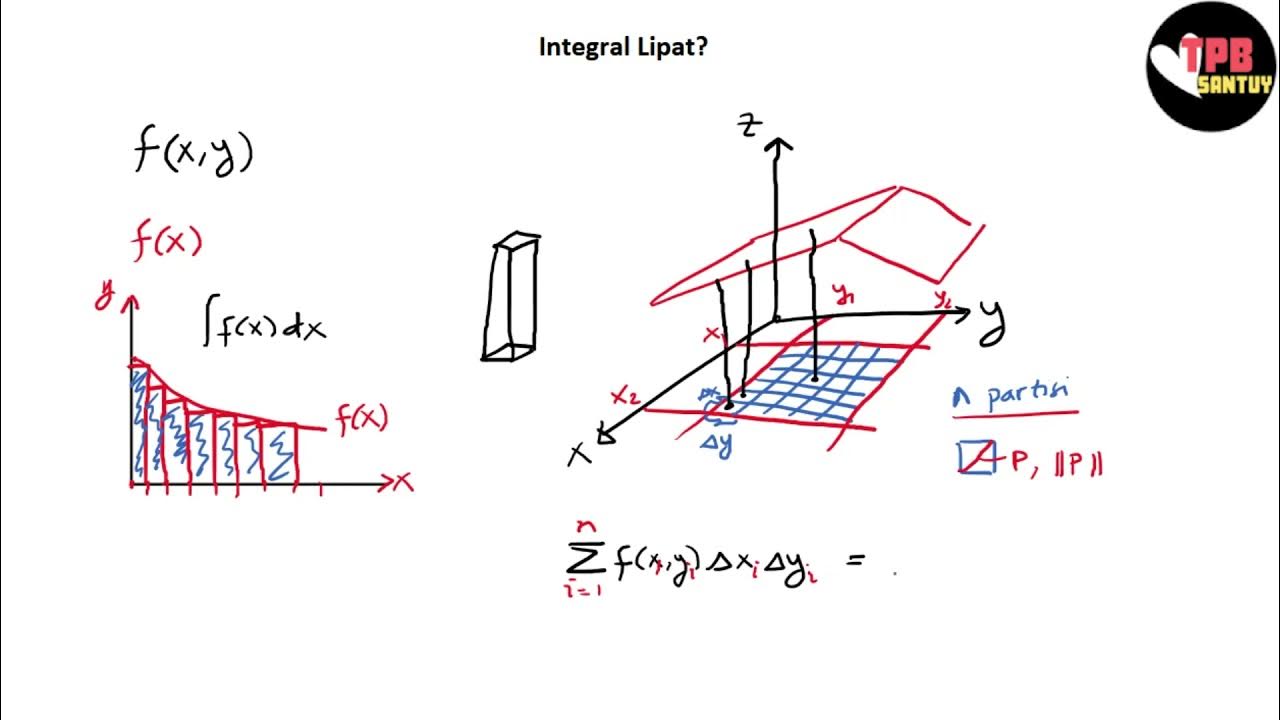
• 😀 The video explains how to calculate a double integral over a region that is a rectangle or square, with a focus on integral limits and boundaries.
• 😀 The region of integration is defined within a coordinate plane, specifically as a rectangle where the sides are parallel to the x and y axes.
• 😀 It discusses the importance of understanding the limits of integration when dealing with simple regions, like rectangles and squares.
• 😀 For regions that are not rectangles or squares, the process of double integration involves considering different integral limits, especially when boundaries are irregular.
• 😀 A key step in the process is graphing the region of integration to determine the exact limits for the double integral.
• 😀 The video emphasizes that the calculation of double integrals involves defining clear boundaries and ensuring that they are applied consistently across the integration.
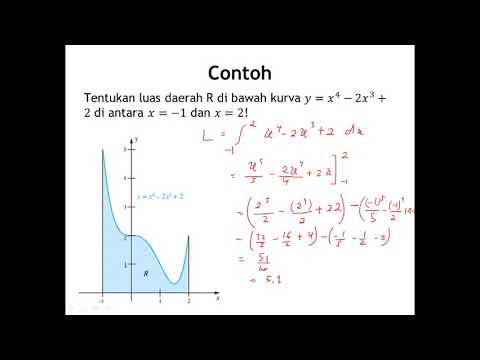
• 😀 Integral limits for a triangular region are explained, with an example of a triangle with vertices at (0, 0), (1, 4), and (0, 4).
• 😀 A line equation for a boundary of a region is derived, such as y = 4x for a line between points (0, 0) and (1, 4).
• 😀 It is highlighted that when performing a double integral, the order of integration (whether integrating with respect to x or y first) depends on the structure of the region.
• 😀 The importance of correctly setting up the integral based on the region's boundaries is stressed, and the result of the integral will vary based on these boundaries.

Q & A

What is the main topic discussed in the video?

The main topic discussed in the video is the concept of double integrals over regions that are not necessarily rectangular, with a focus on integration over triangular regions.

What is a key distinction made regarding the type of regions used in double integrals?

The video distinguishes between double integrals over rectangular regions and those over non-rectangular regions, such as triangles. The integration limits and methods vary based on the shape of the region.

What are the key steps in setting up a double integral for a non-rectangular region?

To set up a double integral for a non-rectangular region, you need to identify the boundaries of the region, express them mathematically, and then determine the appropriate limits for the integration in both the x and y directions.

How is a triangular region described in the video for the double integral?

A triangular region is described by its vertices, which are at points (0, 0), (0, 4), and (1, 4). The region is bounded by lines, and the equation of the line passing through points (0, 0) and (1, 4) is derived as y = 4x.

What is the purpose of determining the equation of the line through points (0, 0) and (1, 4)?

The equation of the line, y = 4x, is used to define the upper boundary of the triangular region in the double integral. This helps to set the correct limits for the integration in the y-direction.

What happens when the region of integration is a rectangle or square?

When the region of integration is a rectangle or square, the double integral is straightforward to set up, as the boundaries are parallel to the coordinate axes, making the limits of integration easier to define.

How does the approach to integration change for non-rectangular regions?

For non-rectangular regions, the limits of integration must be carefully defined according to the boundaries of the region. The integration order (dx first or dy first) may also need to be adjusted based on the geometry of the region.

What is the relationship between the two types of integration discussed: dxdy and dydx?

The video emphasizes that for both dxdy and dydx integrals, the result will be the same as long as the boundaries are properly defined. However, the choice of which variable to integrate first depends on the region's geometry.

Why is it important to carefully define the integration boundaries?

It is important to carefully define the integration boundaries because the correct setup of the limits determines the accuracy of the integral's result, especially for non-rectangular regions where boundaries are not aligned with the axes.

How does the final result of the double integral relate to the volume or area of the region?

The result of the double integral corresponds to the volume under the surface defined by the integrand over the specified region. For a simple function like x + y, the result would represent a volume, whereas for a more complex function, the result would include variables from the integrand.