Transformasi Geometri [Part 3] - Rotasi (Perputaran)

Summary

In this video, Pak Beni explains the concept of rotation in geometry, focusing on the transformation of points and shapes by rotating them around a central point. He covers essential concepts like the angle of rotation, direction (clockwise vs counterclockwise), and how to calculate the new coordinates using formulas. The video provides examples of rotating points by 90°, 180°, and other angles, both clockwise and counterclockwise. Pak Beni also demonstrates how to use rotation formulas to find the new coordinates and solve practice problems, helping viewers understand the principles behind geometric rotations.

Takeaways

• 😀 Rotation (rotasi) is a geometric transformation that turns every point on a shape around a specific center of rotation by a certain angle.
• 😀 The key factors affecting the outcome of a rotation are the angle, direction, and center of rotation.
• 😀 Rotation can be counterclockwise (positive angles) or clockwise (negative angles), depending on the given angle's sign.
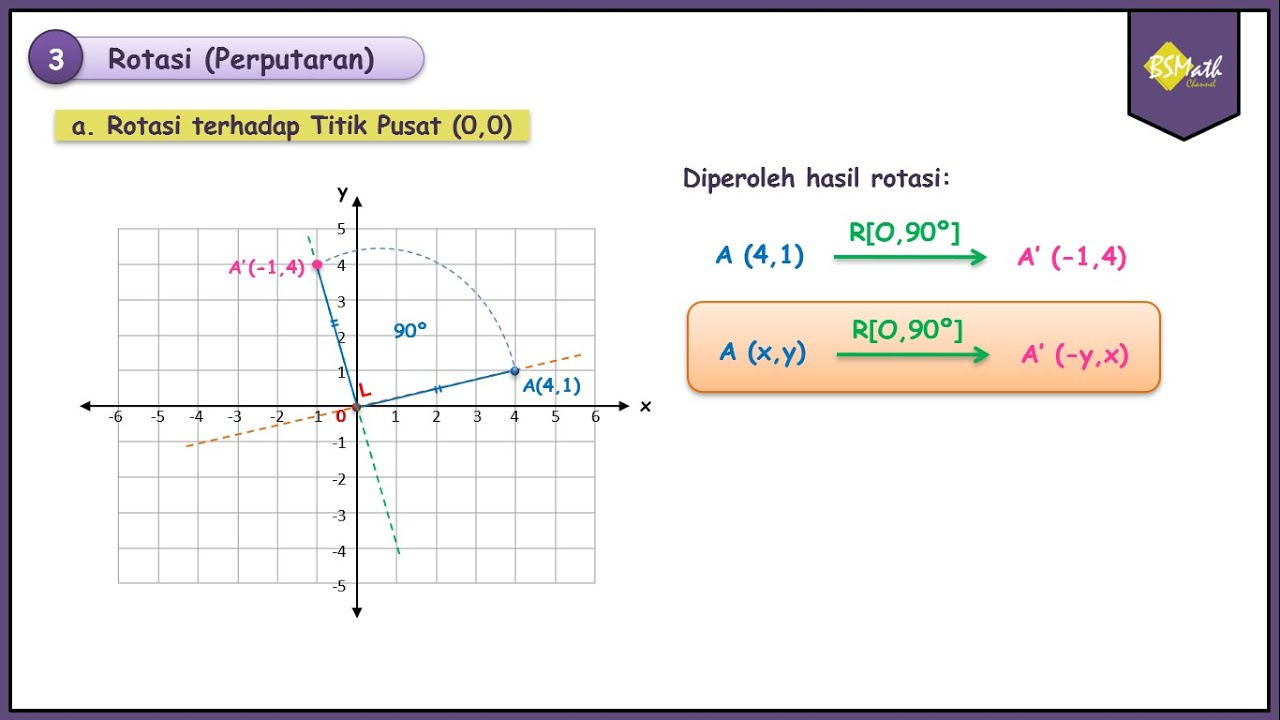
• 😀 When a shape is rotated around the origin (0,0), the coordinates of the points are transformed according to specific formulas based on the rotation angle.
• 😀 For a 90° or -270° counterclockwise rotation, the new coordinates of a point (x, y) become (-y, x).
• 😀 For a -90° or 270° clockwise rotation, the new coordinates of a point (x, y) become (y, -x).
• 😀 A 180° rotation or -180° rotation simply negates both x and y coordinates, turning (x, y) into (-x, -y).
• 😀 The rotation of a point around the origin with different angles results in different transformations of the coordinates.
• 😀 If the rotation's angle is positive, the transformation will be counterclockwise, while a negative angle indicates a clockwise rotation.
• 😀 Practicing with examples, such as rotating points or triangles, helps solidify the understanding of rotation and its formulas.

Q & A

What is the main focus of the video on geometry transformations?

The video focuses on rotation (rotasi) as part of geometry transformations. It explains how to rotate points and shapes around a reference point, specifically detailing the process using different angles.

What key elements affect the result of a rotation transformation?

The three key elements that affect the result of a rotation are the angle, direction, and reference point (center of rotation).

How is rotation defined in the context of geometry transformations?

Rotation is defined as a transformation that rotates every point on a plane or geometric shape by a certain angle and direction around a specific reference point.

What happens when the reference point is changed in a rotation?

When the reference point changes, the result of the rotation also changes. The same shape will rotate differently depending on the location of the reference point.

How can rotation be performed both clockwise and counterclockwise?

Rotation can occur counterclockwise (positive angle) or clockwise (negative angle). The direction is specified by the sign of the angle in the problem.

What is the formula for rotating a point (x, y) by a given angle?

The formula for rotating a point (x, y) by an angle θ around the origin (0, 0) is: For 90° or -270°, the result is (-y, x); for -90° or 270°, the result is (y, -x); for 180° or -180°, the result is (-x, -y).

What is the significance of a positive or negative angle in rotation?

A positive angle indicates a counterclockwise rotation, while a negative angle indicates a clockwise rotation. This is crucial for determining the direction of rotation in a problem.

How do you apply the rotation formula to find the new coordinates of a point?

To apply the rotation formula, substitute the initial coordinates into the respective formula depending on the angle. For example, rotating a point (x, y) by 90° would give the new coordinates as (-y, x).

How do you determine the rotated coordinates of a triangle after a 180° rotation?

To rotate a triangle by 180°, you simply negate the coordinates of each vertex. For example, if a point has coordinates (x, y), after rotation, it becomes (-x, -y). This is applied to each vertex of the triangle.

What are the steps for solving a rotation problem with specific coordinates and an angle?

To solve a rotation problem, first identify the coordinates of the point, determine the angle of rotation, and apply the corresponding rotation formula. Ensure to account for the direction (clockwise or counterclockwise) of the rotation based on the sign of the angle.