ASYIK! Rumus ROTASI. TRANSFORMASI FUNGSI. Matematika Kelas 12 [SMA]
Summary
TLDRThis video covers the topic of transformation, specifically focusing on rotation. It explains how rotation is a form of transformation centered around point O, where positive angles represent counterclockwise rotation and negative angles indicate clockwise rotation. Key formulas are introduced for rotating functions: rotating by 90 degrees (or -270 degrees), -90 degrees (or 270 degrees), and 180 degrees. Each formula describes the transformation of the function under rotation. The video also hints at further examples and applications of these formulas in subsequent videos.
Takeaways
- 🔄 Rotation is a type of transformation, also called 'perputaran' in Indonesian.
- 🌀 Rotation occurs around a center point, commonly referred to as point O.
- ⏱️ Positive rotation is counterclockwise, while negative rotation is clockwise.
- ↪️ A -90-degree rotation means a 90-degree clockwise rotation.
- ↩️ A 90-degree rotation (positive) means a 90-degree counterclockwise rotation.
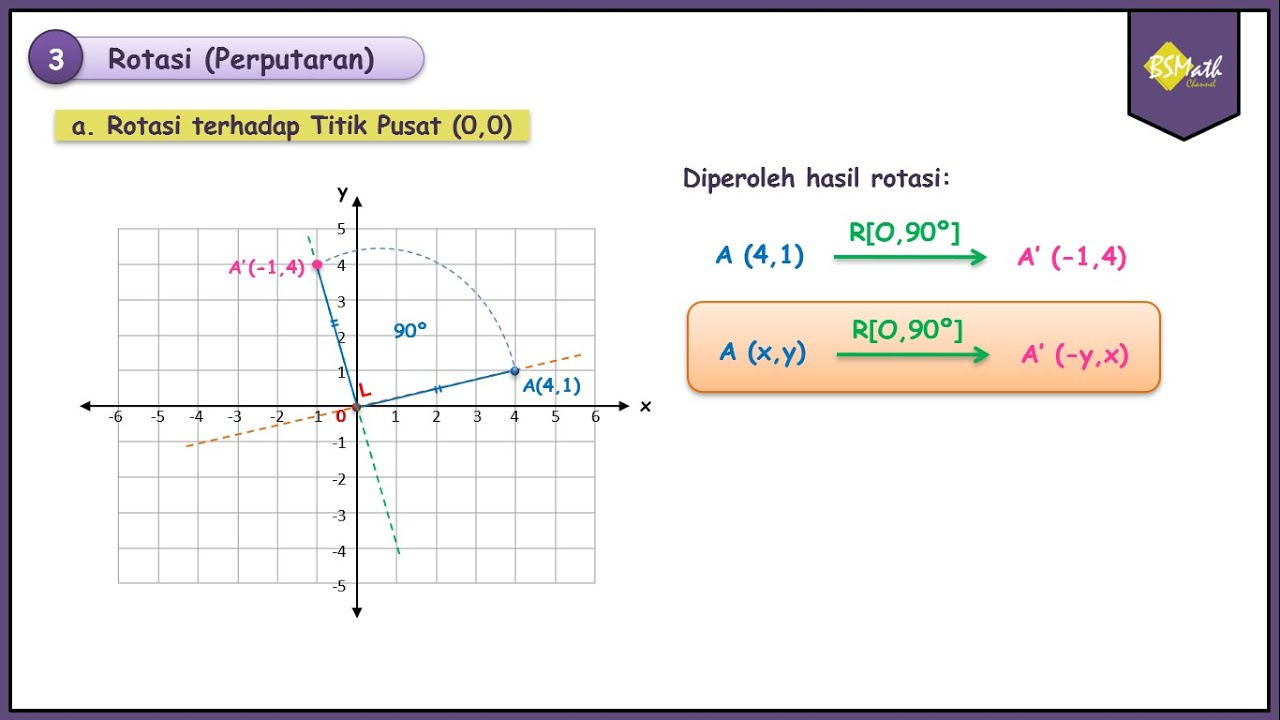
- 📐 First rule: If y = f(x) is rotated around point O by 90 degrees or -270 degrees, the result is x = -f(y).
- 🔄 Second rule: If y = f(x) is rotated around point O by -90 degrees or 270 degrees, the result is x = f(-y).
- 🔄 Third rule: If y = f(x) is rotated around point O by 180 degrees, the result is y = -f(-x).
- 📝 These rotation rules can be applied to various math problems.
- 📹 More examples and explanations can be seen in the following videos.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the transformation of functions, specifically focusing on rotation (or 'perputaran') with respect to a point, typically the origin (O).
What is the meaning of a positive rotation angle?
-A positive rotation angle refers to a rotation counterclockwise, or against the direction of the clock's hands. For example, a 90-degree positive rotation is counterclockwise.
What is the meaning of a negative rotation angle?
-A negative rotation angle refers to a clockwise rotation. For instance, a -90-degree rotation means a 90-degree rotation in the direction of the clock's hands.
How is a function rotated 90 degrees counterclockwise?
-When a function y = f(x) is rotated 90 degrees counterclockwise around point O, its new form is x = -f(y).
What is the transformation rule for a 90-degree clockwise rotation?
-For a 90-degree clockwise rotation (or -90 degrees), the transformation of the function y = f(x) is x = f(-y).
What is the result of rotating a function by 180 degrees?
-When a function y = f(x) is rotated by 180 degrees, its new form is y = -f(-x).
What are the equivalent angles for a 90-degree counterclockwise rotation and a 270-degree clockwise rotation?
-A 90-degree counterclockwise rotation is equivalent to a -270-degree clockwise rotation.
What is the equivalent of a -90-degree rotation in positive angles?
-A -90-degree clockwise rotation is equivalent to a 270-degree counterclockwise rotation.
How does the rotation of functions apply to problem-solving?
-The rotation formulas can be applied to specific problems by transforming functions based on the rotation angle and the center of rotation. This is demonstrated in upcoming video examples.
What is the center of rotation in the transformations described?
-The center of rotation in these transformations is point O, typically the origin of the coordinate system.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Rotasi Hal 34-36 Bab 1 TRANSFORMASI FUNGSI Kelas 12 SMA SMK Kurikulum Merdeka

PEMBUKTIAN TRANSFORMASI | Geometri Transformasi #2

Transformasi Geometri [Part 3] - Rotasi (Perputaran)

Transformasi gabungan

Transformasi Geometri Bagian 3 - Rotasi (Putaran) Matematika Wajib Kelas 11
Rotasi Terhadap Titik Pusat O(0,0) - Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)