Triángulos y polígonos: 2. Solución problema

Recursos Libres de Matemáticas

23 Nov 202001:58

Summary

TLDREn este video, se explica cómo calcular el área de un muro utilizando hexágonos y triángulos. El cálculo empieza con la medición del muro, que tiene una altura de 1.73 metros, dividiéndolo en áreas de hexágonos formados por triángulos. El área total cubierta por los hexágonos es de 10.32 metros cuadrados, y el área restante es de 3.52 metros cuadrados. Finalmente, se calcula la cantidad de pintura necesaria, siendo medio galón para el azul y un cuarto de galón para el celeste, según el área cubierta por cada color.

Takeaways

😀 El muro tiene una altura de 1.73 metros, lo que implica que la mitad de esa medida es aproximadamente 0.86 metros.
😀 El lado de cada hexágono es igual a la base del triángulo que se utiliza en los cálculos, y mide 1 metro.
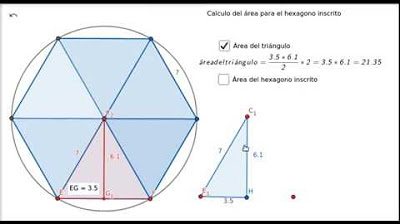
😀 El área de un triángulo se calcula con la fórmula: base por altura dividido entre dos, lo que da como resultado un área de 0.43 metros cuadrados para un triángulo.
😀 Cada hexágono está formado por seis triángulos, por lo que el área total de un hexágono es de 2.58 metros cuadrados.
😀 El área total cubierta por los cuatro hexágonos es 10.32 metros cuadrados.
😀 El área total del muro es de 13.84 metros cuadrados, lo que deja un área no cubierta de 3.52 metros cuadrados.
😀 Para cubrir los 3.52 metros cuadrados restantes, se necesita pintar las áreas que no están ocupadas por los hexágonos.
😀 Se necesitan aproximadamente medio galón de pintura azul para cubrir el área restante.
😀 También se requiere un cuarto de galón de pintura celeste para cubrir el área que no es de color azul.
😀 Un galón de pintura cubre aproximadamente 30 metros cuadrados, medio galón cubre 15 metros cuadrados y un cuarto de galón cubre 7.5 metros cuadrados.
😀 Los cálculos son clave para determinar la cantidad exacta de pintura que se necesita según el área no cubierta.

Q & A

¿Cuánto mide la altura total del muro?
-La altura total del muro es de 1.73 metros.
¿Qué representa la mitad de la altura del muro?
-La mitad de la altura del muro es aproximadamente 0.86 metros, que se usa como la altura de los triángulos dentro del hexágono.
¿Cuánto mide el lado del hexágono y qué relación tiene con la base del triángulo?
-El lado del hexágono mide 1 metro, y es la misma medida que la base de cada triángulo que forma el hexágono.
¿Cuál es la fórmula para calcular el área de un triángulo?
-La fórmula para calcular el área de un triángulo es: Área = (Base × Altura) ÷ 2.
¿Cuál es el área de un triángulo que tiene una base de 1 metro y una altura de 0.86 metros?
-El área del triángulo es 0.43 metros cuadrados, calculado como: (1 × 0.86) ÷ 2.
¿Cuántos triángulos forman un hexágono y qué área total cubren?
-Un hexágono está formado por 6 triángulos, y el área total de cada hexágono es de 2.58 metros cuadrados (6 × 0.43).
¿Qué área total cubren los 4 hexágonos?
-Los 4 hexágonos cubren un área total de 10.32 metros cuadrados (4 × 2.58).
¿Cuál es el área total del muro y cuál es la diferencia con el área cubierta por los hexágonos?
-El área total del muro es de 13.84 metros cuadrados, y la diferencia con el área cubierta por los hexágonos es de 3.52 metros cuadrados.
¿Cuánto cubren los diferentes tamaños de galones de pintura?
-Un galón cubre 30 metros cuadrados, medio galón cubre 15 metros cuadrados, y un cuarto de galón cubre 7.5 metros cuadrados.
¿Cuántos galones de pintura se necesitan para cubrir los hexágonos y los espacios en celeste?
-Para cubrir los hexágonos (10.32 m²) se necesita medio galón de pintura azul, y para cubrir los espacios en celeste (3.52 m²) se necesita un cuarto de galón de pintura celeste.