90. Ecuación diferencial de coeficientes constantes (Con una raíz igual a cero) EJERCICIO RESUELTO
Summary
TLDREn este vídeo, se explica cómo resolver la ecuación diferencial de segundo orden y lineal 'y'' - 5y' = 0'. Se propone una solución exponencial y se obtiene la ecuación característica 'r^2 - 5r = 0'. Al factorizar, se encuentran los valores de 'r' (0 y 5), y se derivan dos soluciones: y1 = 1 y y2 = e^(5x). La solución general es una combinación lineal de ambas, y = c1*y1 + c2*y2. Además, se menciona que en futuras ecuaciones, las soluciones pueden ser reales repetidas o complejas.
Takeaways
- 📘 La ecuación diferencial presentada es de segundo orden, lineal, homogénea y con coeficientes constantes.
- 💡 Para resolver este tipo de ecuaciones, se propone una solución de forma exponencial: y = e^rx.
- 🛠️ Se obtiene la ecuación característica al sustituir la solución en la ecuación diferencial y factorizar la exponencial.
- 🧮 La ecuación característica se forma al sustituir las derivadas por términos en r: r² para la segunda derivada, r para la primera, y el coeficiente para y.
- ✂️ Se puede factorizar una r común de la ecuación característica, resultando en: r(r - 5) = 0.
- ✅ Las soluciones de la ecuación característica son r = 0 y r = 5, generando dos soluciones para la ecuación diferencial.
- 🧑🏫 La primera solución es y1 = 1, obtenida al sustituir r = 0 en la solución exponencial.
- 🚀 La segunda solución es y2 = e^(5x), obtenida al sustituir r = 5 en la solución exponencial.
- 📐 La solución general de la ecuación diferencial es una combinación lineal de ambas soluciones: y = c1 + c2 * e^(5x).
- 🔮 En futuros vídeos, se abordarán casos donde la ecuación característica tiene soluciones repetidas o complejas.
Q & A
¿Qué tipo de ecuación diferencial se resuelve en el vídeo?
-Se resuelve una ecuación diferencial de segundo orden, lineal y de coeficientes constantes, que es homogénea.
¿Cómo se propone una solución inicial para la ecuación diferencial mencionada?
-Se propone una solución de forma exponencial, de la forma \( y = e^{rx} \).
¿Qué es la ecuación característica y cómo se obtiene?
-La ecuación característica es una ecuación algebraica que se obtiene a partir de la sustitución de la solución propuesta en la ecuación diferencial original.
¿Cómo se derivan las soluciones de la ecuación característica?
-Se derivan las soluciones de la ecuación característica al factorizar y resolver las ecuaciones resultantes de primer grado que surgen al igualar a cero el producto de los factores.
¿Cuáles son las soluciones obtenidas para la ecuación característica en el ejemplo?
-Las soluciones obtenidas para la ecuación característica son \( r = 0 \) y \( r = 5 \).
¿Qué solución se obtiene al sustituir \( r = 0 \) en la ecuación diferencial?
-Al sustituir \( r = 0 \), se obtiene la solución \( y_1 = 1 \).
¿Cuál es la segunda solución y cómo se obtiene?
-La segunda solución es \( y_2 = e^{5x} \) y se obtiene al sustituir \( r = 5 \) en la ecuación diferencial.
¿Cómo se expresa la solución general de la ecuación diferencial?
-La solución general se expresa como una combinación lineal de las soluciones particulares, es decir, \( y = c_1 \cdot y_1 + c_2 \cdot y_2 \).
¿Qué ocurre si la ecuación característica tiene soluciones complejas?
-Si la ecuación característica tiene soluciones complejas, se deben aplicar métodos adicionales para resolver la ecuación diferencial, como se explicará en un vídeo futuro.
¿Cómo se pueden verificar que las soluciones propuestas son correctas?
-Se pueden verificar las soluciones derivando y sustituyendo en la ecuación diferencial original para confirmar que satisfacen la ecuación.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
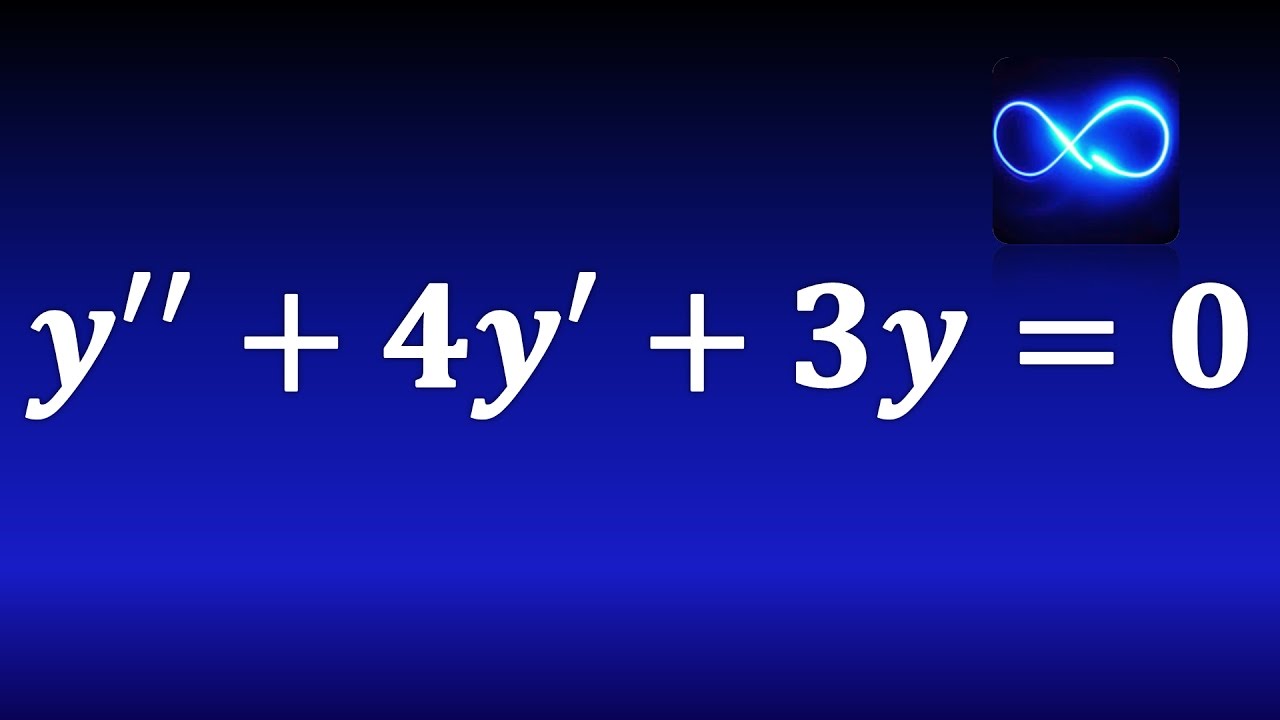
87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
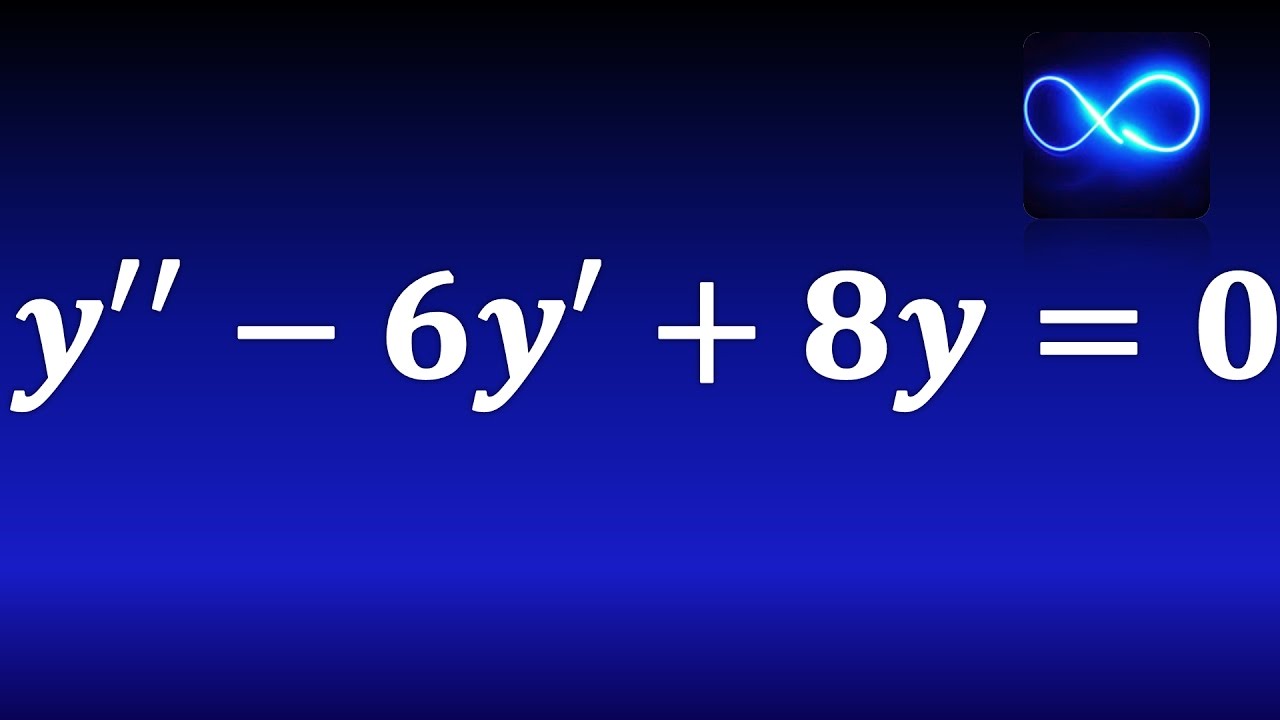
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

96. Ecuación diferencial de coeficientes constantes, raíces repetidas. EJERCICIO RESUELTO.

Ecuaciones diferenciales lineales - no lineales
Modelado matemático de péndulo simple
Introducción a las intersecciones con los ejes
5.0 / 5 (0 votes)
