Modelado matemático de péndulo simple
Summary
TLDREste video ofrece una explicación detallada sobre cómo obtener el modelo matemático de un péndulo simple. Se comienza estableciendo restricciones como la longitud del péndulo, la masa concentrada en un extremo y la ausencia de fricción o fuerzas externas. Se describe el marco de referencia y las leyes físicas de Newton que rigen el sistema. Seguidamente, se realiza un análisis de fuerzas y se plantea un sistema de ecuaciones para determinar la tensión y el peso como fuerzas actuantes sobre el péndulo. El proceso incluye la derivación de las posiciones y aceleraciones en los ejes x e y, y la simplificación de la ecuación para obtener una ecuación diferencial de segundo orden no lineal. Finalmente, se muestra que la dinámica del péndulo depende principalmente de la longitud y la gravedad, y se presenta la ecuación simplificada del modelo matemático.
Takeaways
- 📚 Se discute cómo obtener un modelo matemático para un péndulo simple.
- 📐 Se establece un diagrama para expresar las variables del sistema mecánico de tipo rotacional.
- ⚙️ Se describen las restricciones del modelo, como la longitud del péndulo y la masa concentrada en un extremo.
- 🚫 Se asume ausencia de fricción y de excitación externa en el sistema.
- 🔄 Se establece que el movimiento del péndulo es en un plano determinado y se define un marco de referencia.
- 📉 Se describen las leyes físicas de Newton para el sistema rotacional y se establecen las fuerzas en los ejes x e y.
- 📈 Se realiza un análisis de fuerzas en el diagrama de cuerpo libre del péndulo, considerando peso y tensión.
- 🔄 Se plantean ecuaciones para el movimiento en los ejes x e y, relacionando tensión, peso y aceleración.
- 🧩 Se simplifican las ecuaciones para reducir el número de incógnitas y relacionarlas con ángulos y derivadas.
- 📉 Se llega a una ecuación diferencial de segundo orden no lineal que describe el movimiento del péndulo.
- 📚 Se concluye que la dinámica del péndulo depende de la longitud y la gravedad, y no de la masa.
Q & A
¿Qué se busca obtener en el video?
-El objetivo del video es obtener un modelo matemático para un péndulo simple.
¿Cuáles son las restricciones iniciales establecidas para el modelo del péndulo?
-Las restricciones incluyen la longitud del péndulo, considerar la barra como un cuerpo rígido, la masa cargada en un extremo, ausencia de fricción y de excitación externa.
¿Cómo se define el movimiento del péndulo según la intuición?
-El movimiento del péndulo, por intuición, sería una trayectoria semicircular.
¿En qué plano se da el movimiento del péndulo según el script?
-El movimiento del péndulo se da en un plano definido por el marco de referencia en el punto de unión del péndulo con un elemento fijo.
¿Cómo se establecen las direcciones de los ejes en el marco de referencia del péndulo?
-Las direcciones de los ejes en el marco de referencia están definidas de tal manera que el eje x apunte hacia la derecha y el eje y hacia arriba, pero es importante destacar que esta asignación es arbitraria.
¿Qué tipo de leyes físicas describen el modelo mecánico del péndulo?
-Las leyes físicas que describen el modelo mecánico del péndulo son las leyes de Newton para movimientos rotacionales.
¿Cuáles fuerzas actúan sobre el péndulo y cómo se relacionan con las ecuaciones de movimiento?
-Las fuerzas que actúan sobre el péndulo son la gravedad (peso) y la tensión. Estas fuerzas se relacionan con las ecuaciones de movimiento a través de la suma de fuerzas en los ejes x e y.
¿Cómo se relaciona la tensión con el movimiento del péndulo en las ecuaciones?
-La tensión en el péndulo tiene componentes tanto en el eje x como en el eje y, y estas componentes están relacionadas con el ángulo del péndulo a través de funciones trigonométricas como el seno.
¿Por qué es necesario simplificar las ecuaciones en el análisis del péndulo?
-Es necesario simplificar las ecuaciones para reducir la cantidad de incógnitas y facilitar la relación entre ellas, lo que permite obtener una ecuación más manejable y sencilla.
¿Qué tipo de ecuación diferencial se obtiene al final del análisis del péndulo?
-Se obtiene una ecuación diferencial de segundo orden y no lineal, ya que involucra la función trigonométrica del ángulo.
¿Cómo se muestra que la dinámica del péndulo no depende de la masa en la ecuación final?
-Al simplificar la ecuación diferencial y eliminar la masa de la ecuación, se muestra que la dinámica del péndulo depende principalmente de la longitud y la gravedad.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

(cũ) Votol Calibrate - Hiệu chỉnh thông số Flux động cơ trên ECU Votol

Programación Lineal Problema de Transporte 1

Problema de programación por metas

Sistema de ecuaciones lineales 2x2, el problema de las monedas | Planteamiento de ecuaciones 10
DELIMITACION DE UNA CUENCA EN ARCGIS, DESCARGA DE CARTAS NACIONALES,
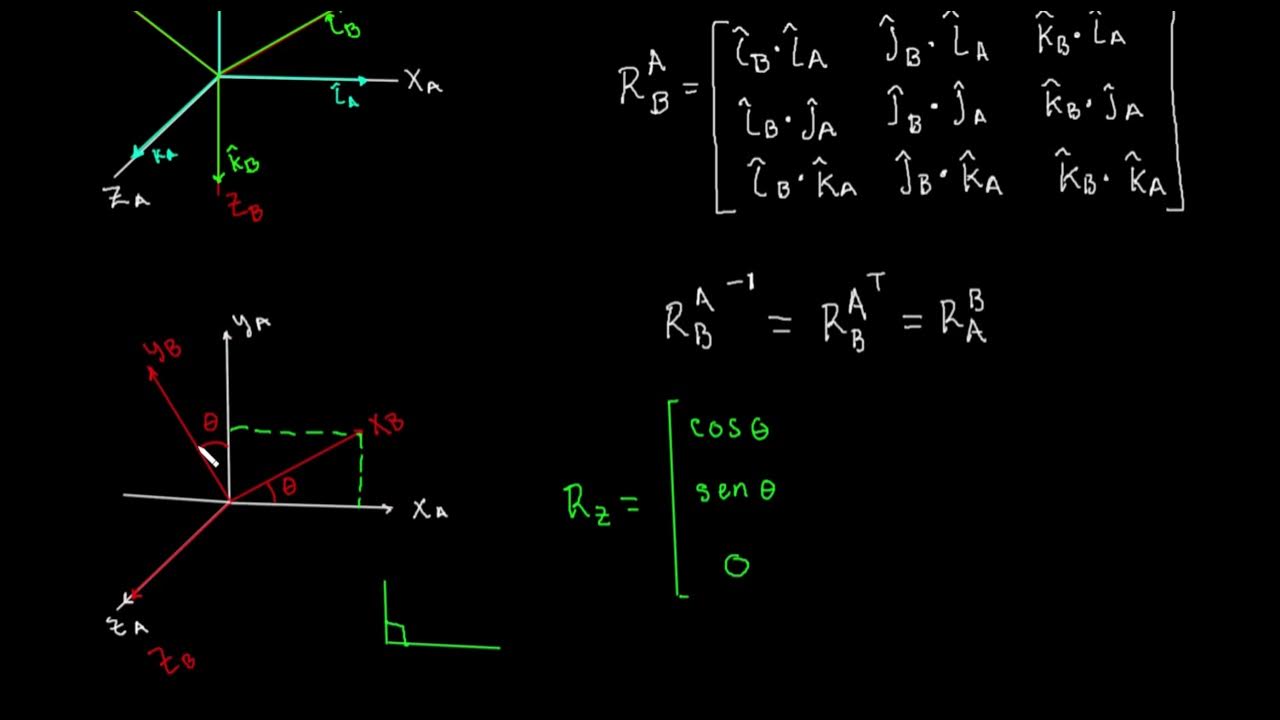
Matrices de rotación en 3D de x, y, z
5.0 / 5 (0 votes)
