96. Ecuación diferencial de coeficientes constantes, raíces repetidas. EJERCICIO RESUELTO.
Summary
TLDREn este video, se resuelve una ecuación diferencial homogénea de segundo orden con coeficientes constantes. Se introduce la solución propuesta \( y = e^{r \cdot x} \), derivando la ecuación característica. La ecuación cuadrática resultante se resuelve utilizando la fórmula general, obteniendo una única solución para \( r \). Para hallar una segunda solución linealmente independiente, se multiplica la primera por \( x \). Finalmente, se presenta la solución general combinando ambas soluciones. El video concluye con un ejercicio de ecuación diferencial de tercer orden para resolver de manera similar.
Takeaways
- 📘 La ecuación diferencial tratada en el video es de segundo orden, homogénea y de coeficientes constantes.
- 🔍 Se propone una solución de la forma y = e^(r*x) para resolver la ecuación diferencial.
- 📐 Se forma una ecuación característica al igualar el coeficiente de la segunda derivada de y a r^2, la primera derivada a r y la función y a cero.
- 🔢 Se resuelve la ecuación característica de segundo grado usando la fórmula general de解二次方程.
- 📈 Se calcula el valor de r utilizando la fórmula r = (-B ± √(B^2 - 4AC)) / 2A, donde A=4, B=-12 y C=9.
- 🔄 Se obtiene un único valor para r, que es 3/2, indicando una solución de la ecuación diferencial.
- 🌐 Se obtiene una solución de la ecuación diferencial sustituyendo el valor de r, que es y = e^(3/2*x).
- 📝 Se menciona que para una solución general de una ecuación diferencial de segundo orden se necesitan dos soluciones linealmente independientes.
- 🔄 Se obtiene una segunda solución multiplicando la primera solución por x, dando lugar a y = x * e^(3/2*x).
- 🔑 Se presenta la solución general como una combinación lineal de las dos soluciones obtenidas: y = C1 * e^(3/2*x) + C2 * x * e^(3/2*x).
- 🔍 Se invita a los espectadores a intentar resolver un ejercicio de ecuación diferencial de tercer orden antes de ver el siguiente video.
Q & A
¿Qué tipo de ecuación diferencial se resuelve en el video?
-Se resuelve una ecuación diferencial de segundo orden, homogénea y de coeficientes constantes.
¿Cuál es la forma general de las soluciones para una ecuación diferencial de segundo orden con coeficientes constantes?
-Las soluciones generalmente tienen la forma y = e^(r*x).
¿Cómo se obtiene la ecuación característica de una ecuación diferencial?
-Se reemplaza la segunda derivada de y por r^2, la primera derivada de y por r y a la función y simplemente se coloca un 1 en lugar de y.
¿Cuál es la ecuación característica para la ecuación diferencial dada en el video?
-La ecuación característica es 4r^2 - 12r + 9 = 0.
¿Cómo se resuelve la ecuación algebraica de segundo grado obtenida?
-Se resuelve mediante la fórmula general o mediante factorización. En el video se usa la fórmula general.
¿Cuál es la fórmula general para resolver una ecuación de segundo grado?
-La fórmula general es x = (-b ± √(b^2 - 4ac)) / (2a).
¿Cuál es el valor de 'a', 'b' y 'c' en la ecuación característica?
-En la ecuación característica, 'a' vale 4, 'b' vale -12 y 'c' vale 9.
¿Cuál es el resultado de la ecuación característica resuelta?
-El resultado es r = 3/2, lo que indica una única solución.
¿Cómo se obtiene la primera solución de la ecuación diferencial?
-La primera solución se obtiene sustituyendo el valor de r en la forma y = e^(r*x), dando como resultado y = e^(3/2*x).
¿Cómo se obtiene la segunda solución de la ecuación diferencial?
-La segunda solución se obtiene multiplicando la primera solución por x, dando como resultado x * e^(3/2*x).
¿Cómo se escribe la solución general de la ecuación diferencial?
-La solución general se escribe como una combinación lineal de las dos soluciones obtenidas: y = C1 * e^(3/2*x) + C2 * x * e^(3/2*x).
¿Qué significa que las soluciones sean linealmente independientes?
-Significa que no se puede expresar una solución como una combinación lineal de la otra, lo cual es necesario para escribir la solución general de una ecuación diferencial de segundo orden.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
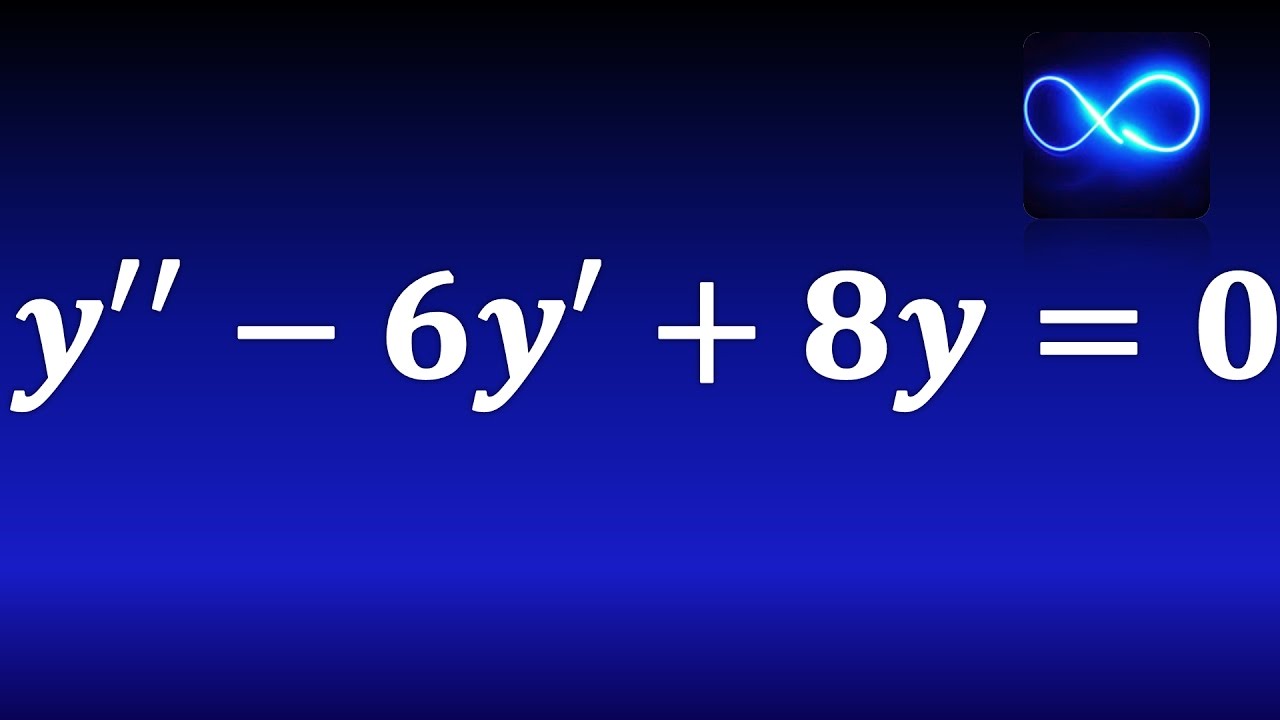
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
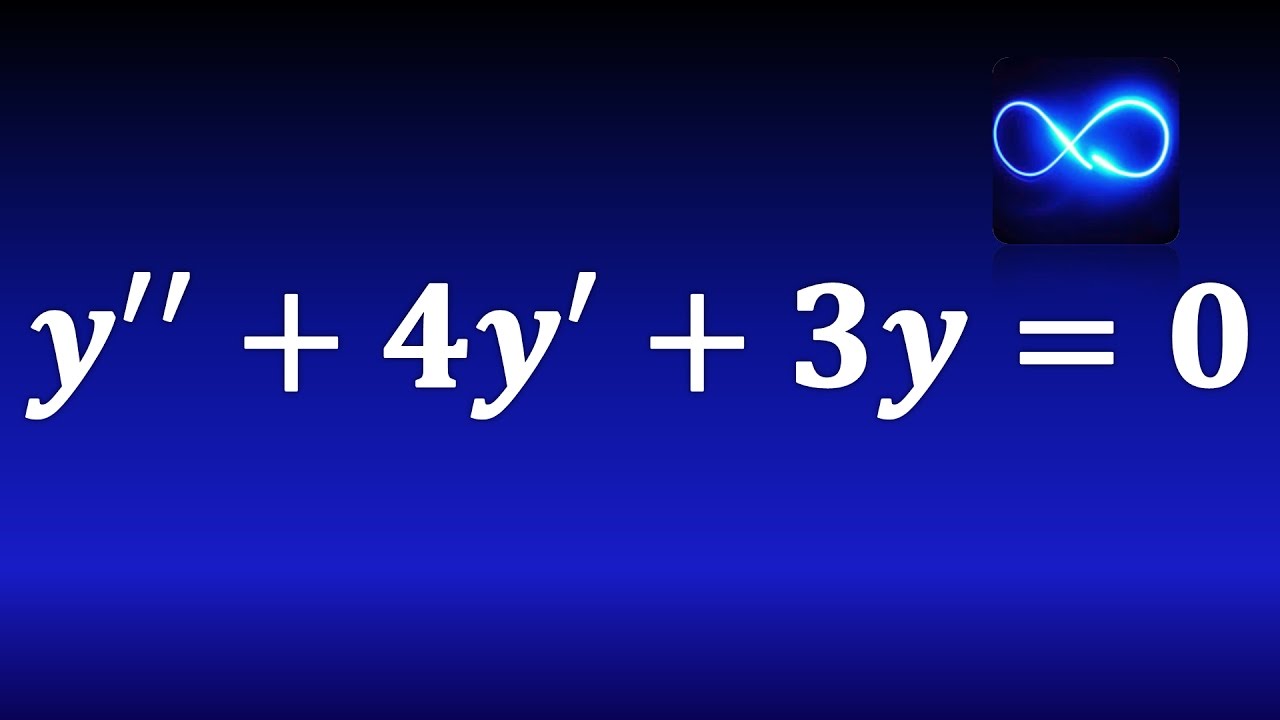
87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
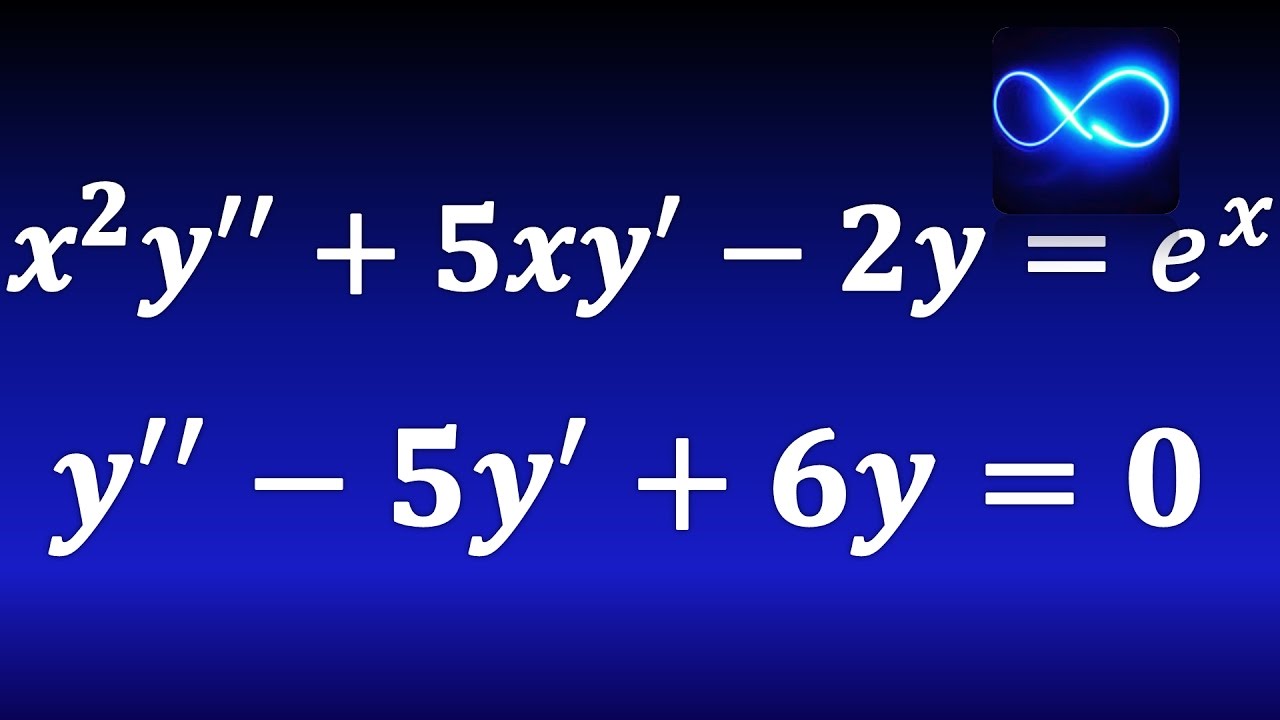
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

Sistema Masa Resorte Multiple

Ecuaciones diferenciales lineales - no lineales

Ecuaciones diferenciales Homogéneas | Ejemplo 1
5.0 / 5 (0 votes)
