Ecuaciones diferenciales lineales - no lineales
Summary
TLDREste video educativo se centra en la identificación de ecuaciones diferenciales lineales y no lineales. Se explica que una ecuación diferencial es lineal si la variable dependiente y sus derivadas no están elevadas a un exponente diferente a uno y si los coeficientes de las derivadas no incluyen la variable dependiente. Se utilizan ejemplos para ilustrar cómo reconocer si una ecuación diferencial es lineal, subrayando la importancia de examinar la variable dependiente y sus derivadas en relación con los coeficientes y cualquier operación matemática aplicada.
Takeaways
- 😀 Las ecuaciones diferenciales lineales son aquellas en las que la variable dependiente y sus derivadas no están elevadas a ningún exponente distinto de uno.
- 🎓 Se define una ecuación como lineal si la variable independiente (generalmente x) y la variable dependiente (generalmente y) están elevadas a la primera potencia o a la cero.
- 📘 Las ecuaciones que incluyen términos con variables elevadas a potencias mayores que uno, o que incluyen funciones trigonométricas o logarítmicas, no son lineales.
- 🔍 Para identificar si una ecuación diferencial es lineal, es crucial observar si la variable dependiente o sus derivadas están afectadas por operaciones que las elevan a un exponente distinto de uno o las colocan en un denominador.
- 📌 Los coeficientes en una ecuación diferencial lineal deben depender únicamente de la variable independiente, y no de la variable dependiente o sus derivadas.
- ✏️ En la notación de ecuaciones diferenciales, la variable que aparece en la parte superior de una derivada indica que esa es la variable dependiente.
- 📐 Las ecuaciones de segundo grado, como aquellas que incluyen términos cuadráticos, no son consideradas lineales en el contexto de las ecuaciones diferenciales.
- 📚 El orden de una ecuación diferencial se determina por el grado más alto de la derivada de la variable dependiente que aparece en la ecuación.
- 👨🏫 El reconocimiento de ecuaciones lineales en diferenciales se basa en la ausencia de funciones no lineales, como seno, coseno, tangente, o cualquier otra función que afecte a la variable dependiente o sus derivadas.
- 📝 Se enfatiza la importancia de la práctica para discernir si una ecuación diferencial es lineal o no, mediante el análisis de múltiples ejemplos y la aplicación de los conceptos aprendidos.
Q & A
¿Qué es una ecuación diferencial y cómo se reconoce si es lineal o no?
-Una ecuación diferencial es una que incluye derivadas de una función, y para ser lineal, debe cumplir con ciertas condiciones: la variable dependiente y sus derivadas deben estar elevadas a la primera potencia, los coeficientes de la variable dependiente y sus derivadas deben ser constantes o funciones solo de la variable independiente, y no deben haber operaciones como exponentes, seno, coseno, entre otras, aplicadas a la variable dependiente o sus derivadas.
¿Cuáles son las características de una ecuación lineal en términos de variables?
-En una ecuación lineal, tanto la variable independiente como la dependiente deben estar elevadas a la primera potencia, es decir, no deben estar elevadas a cero ni a un exponente diferente de uno.
¿Qué significa que los coeficientes de una ecuación diferencial lineal dependan de la variable independiente?
-Esto significa que los coeficientes, que son los números que multiplican a la variable dependiente y sus derivadas, pueden ser constantes o pueden depender de la variable independiente, pero no de la variable dependiente.
¿Por qué no se consideran ecuaciones diferenciales aquellas que no incluyen derivadas?
-Ecuaciones que no incluyen derivadas no son ecuaciones diferenciales porque las ecuaciones diferenciales se definen por la presencia de al menos una derivada de una función.
¿Qué pasa si la variable dependiente en una ecuación diferencial está elevada a un exponente diferente de uno?
-Si la variable dependiente o alguna de sus derivadas está elevada a un exponente diferente de uno, como al cuadrado o al cubo, la ecuación no es lineal.
¿Cómo se identifica la variable dependiente en una ecuación diferencial?
-La variable dependiente es la que aparece en la parte superior de la derivada, por ejemplo, en una derivada notada como 'dy/dx', 'y' es la variable dependiente.
¿Qué significa que una ecuación sea de segundo grado en el contexto de ecuaciones diferenciales?
-Una ecuación de segundo grado en ecuaciones diferenciales se refiere a una ecuación que tiene la segunda derivada de la variable dependiente, pero no cumple con los criterios de ser lineal.
¿Cuál es la importancia de las operaciones en la variable dependiente para determinar si una ecuación diferencial es lineal?
-Las operaciones en la variable dependiente, como el seno, el coseno, el logaritmo, o cualquier otra función trigonométrica o algebraica, invalidan la linealidad de la ecuación diferencial si se aplican a la variable dependiente o sus derivadas.
¿Qué ocurre si la ecuación diferencial incluye una fracción con la variable dependiente en el denominador?
-Si la variable dependiente o alguna de sus derivadas está en el denominador de una fracción, la ecuación diferencial no es lineal.
¿Cómo se determina si una ecuación diferencial es de primer grado?
-Una ecuación diferencial es de primer grado si solo incluye la primera derivada de la variable dependiente y esta derivada, así como la variable dependiente, no están elevadas a ningún exponente distinto de uno.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
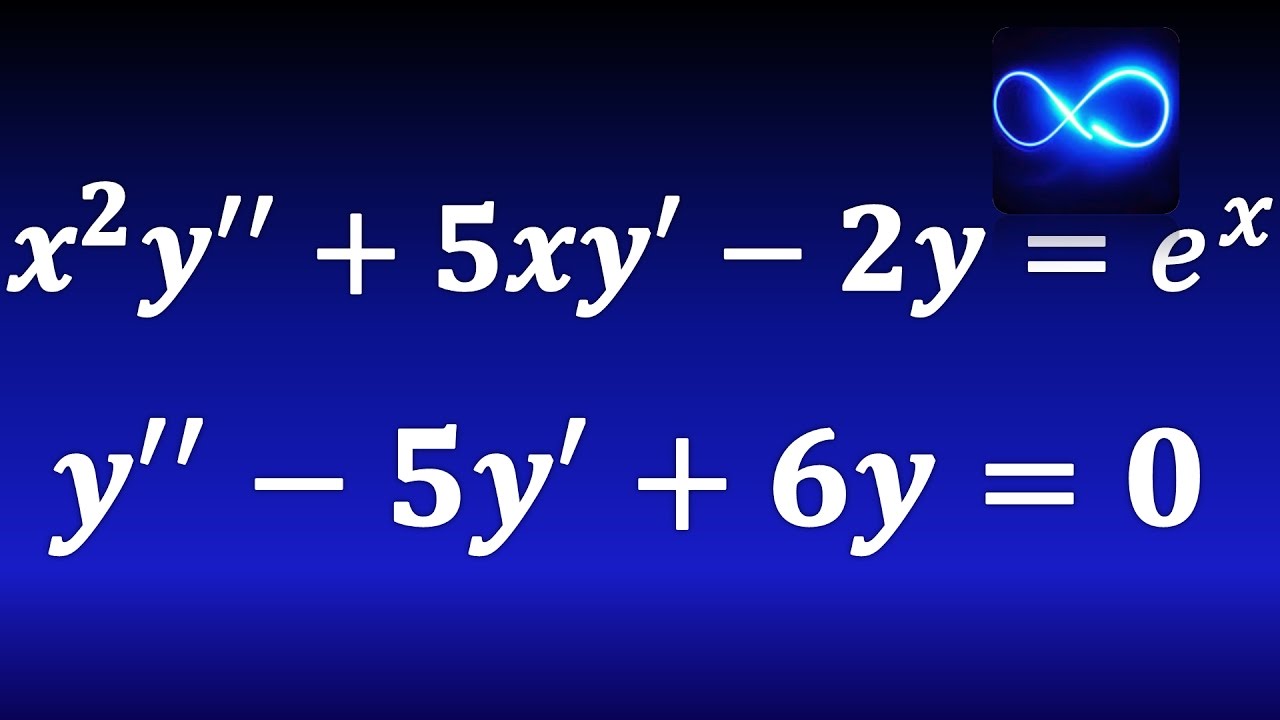
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

DEFINICIÓN DE SISTEMAS DE ECUACIONES LINEALES
Método de la balanza para ecuaciones lineales.

Orden de una Ecuación Diferencial

79. Funciones linealmente independientes ¿qué son? CON EJEMPLOS

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?
5.0 / 5 (0 votes)
