Video Explicativo - Formulación y Planteamiento del Problema
Summary
TLDREl guion del video explica un problema de programación lineal en el que una compañía de pinturas debe maximizar sus ingresos diarios. Se plantea un modelo matemático con variables para la producción de pinturas interiores (XI) y exteriores (XE), sujeto a restricciones de materia prima y demanda. La función objetivo es maximizar las utilidades basadas en los precios de venta. Se presentan las restricciones y la condición de no negatividad para las variables de decisión, para resolver el problema de optimización.
Takeaways
- 🏭 La compañía tiene una pequeña fábrica de pinturas para interior y exterior.
- 🛠️ Se utilizan dos materiales básicos, A y B, para la producción de las pinturas.
- 🚫 La disponibilidad máxima de materia prima A es de 8 toneladas diarias.
- 📊 La demanda de pintura para interiores no puede superar en más de una tonelada a la de exteriores.
- 💰 El precio de la pintura exterior es de $3000 y el de la interior es de $2000 por tonelada.
- 🔢 Se plantea un problema de programación lineal para maximizar las utilidades.
- 📝 Se identifican dos variables de decisión: XE (pintura exterior) y XI (pintura interior).
- 📈 La función objetivo es maximizar Z = 3000XE + 2000XI.
- 🚦 Las restricciones son: XE + 2XI ≤ 6, 2XI ≤ 8, XE - XI ≤ 1, y XI ≤ 2.
- 📋 La condición de no negatividad impone que XE y XI deben ser mayores o iguales a cero.
- 📚 El objetivo es resolver el problema de programación lineal para determinar la cantidad óptima de pinturas a producir.
Q & A
¿Qué tipo de empresa se describe en el guión del video?
-Se describe una compañía que posee una pequeña fábrica de pinturas para interior y exteriores de casa.
¿Cuáles son los materiales básicos utilizados para producir las pinturas?
-Los materiales básicos utilizados son 'A' y 'B'.
¿Cuál es la disponibilidad máxima diaria de material 'A' para la producción de pinturas?
-La disponibilidad máxima diaria de material 'A' es de 8 toneladas.
¿Cuántas toneladas de materia prima 'A' se necesitan para producir una tonelada de pintura para exteriores y para interiores?
-Se necesitan 1 tonelada de materia prima 'A' para producir una tonelada de pintura para exteriores y 2 toneladas para interiores.
¿Cuántas toneladas de materia prima 'B' son necesarias para la pintura para exteriores y para interiores?
-Se necesitan 2 toneladas de materia prima 'B' para la pintura para exteriores y 1 tonelada para interiores.
¿Cuál es la relación establecida por el estudio de mercado entre la demanda de pinturas para interiores y exteriores?
-La demanda diaria de pinturas para interiores no puede ser mayor que la de pinturas para exteriores en más de una tonelada.
¿Cuál es la demanda máxima diaria de pintura para interiores según el estudio de mercado?
-La demanda máxima diaria de pintura para interiores está limitada a dos toneladas.
¿Cuál es el precio al mayoreo por tonelada para las pinturas de exteriores y para interiores?
-El precio al mayoreo es de tres mil dólares por tonelada para la pintura de exteriores y dos mil dólares para la pintura de interiores.
¿Cuáles son las variables de decisión en el problema planteado?
-Las variables de decisión son XE, la cantidad de pinturas para exteriores, y XI, la cantidad de pinturas para interiores.
¿Cuál es la función objetivo que se busca maximizar en el problema de programación lineal?
-La función objetivo es maximizar las utilidades, representadas por Z = 3000 * XE + 2000 * XI.
¿Cuáles son las restricciones establecidas para la producción de pinturas?
-Las restricciones son: XE + 2XI ≤ 6, 2XI ≤ 8, XE - XI ≤ 1, y XI ≤ 2, con la condición de no negatividad para XE y XI.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Problema de la mochila | Knapsack Problem | Programación lineal
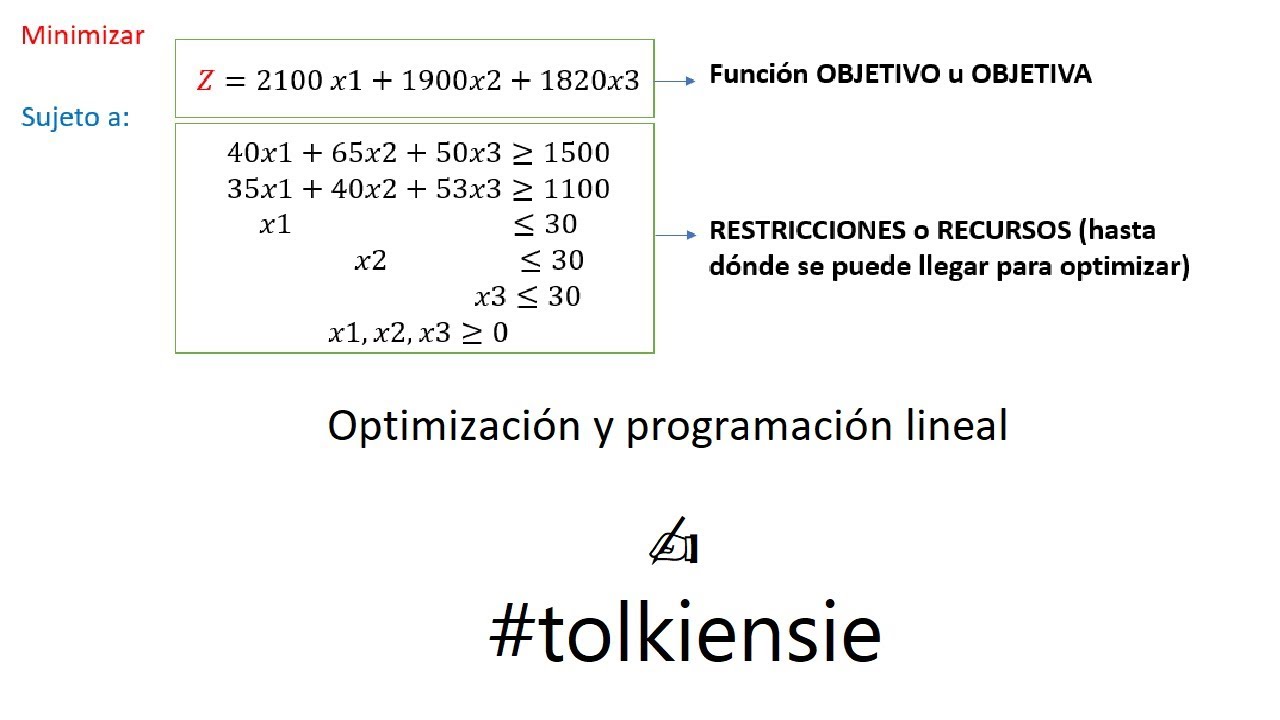
🔴PROGRAMACIÓN LINEAL partes restricciones solución método gráfico 2024 Optimización Max minimizar
Conceptos teóricos de Macros y VBA

Programación Lineal Mesas y Sillas ejemplo1

PASO A PASO PARA HACER EL PLANTEAMIENTO DEL PROBLEMA DE LA TESIS

Problema de programación por metas
5.0 / 5 (0 votes)
