Programación Lineal Mesas y Sillas ejemplo1
Summary
TLDREste video explica cómo resolver un problema de programación lineal utilizando el método gráfico. El ejemplo describe un negocio de fabricación de mesas y sillas, donde se busca maximizar la ganancia respetando las limitaciones de tiempo en los departamentos de corte y ensamble. Se detallan las variables de decisión, la función objetivo, las restricciones y cómo graficar las ecuaciones para encontrar la solución óptima. Finalmente, se utiliza la herramienta Solver para verificar los resultados, encontrando que la producción óptima es 60 mesas y 30 sillas, con una ganancia máxima de 5,400 USD.
Takeaways
- 😀 El problema presentado es sobre programación lineal para maximizar las ganancias en la fabricación de sillas y mesas.
- 😀 Se definen dos variables de decisión: X1 para mesas y X2 para sillas.
- 😀 La función objetivo es maximizar la ganancia, expresada como Z = 50X1 + 80X2.
- 😀 El problema incluye restricciones de tiempo para los departamentos de corte (120 horas) y ensamble (90 horas).
- 😀 En el departamento de corte, cada mesa consume 1 hora y cada silla consume 2 horas.
- 😀 En el departamento de ensamble, tanto las mesas como las sillas consumen 1 hora cada una.
- 😀 Las restricciones se expresan en dos ecuaciones: X1 + 2X2 ≤ 120 (corte) y X1 + X2 ≤ 90 (ensamble).
- 😀 Las variables deben ser mayores o iguales a 0, ya que no se puede producir una cantidad negativa de mesas o sillas.
- 😀 Se realiza una gráfica de las restricciones para encontrar la combinación óptima de producción.
- 😀 La solución óptima es producir 60 mesas y 30 sillas, lo que da una ganancia máxima de 5,400 dólares.
- 😀 El método Solver en Excel también confirma el resultado óptimo de 60 mesas y 30 sillas, con la misma ganancia máxima de 5,400 dólares.
Q & A
¿Cuál es el objetivo principal del ejemplo de programación lineal presentado en el video?
-El objetivo principal es determinar la cantidad de mesas y sillas a producir para maximizar la ganancia, respetando las restricciones de tiempo disponibles en los departamentos de corte y ensamble.
¿Qué significa la variable 'x1' en el contexto de este ejemplo?
-La variable 'x1' representa el número de mesas que se van a producir en el negocio.
¿Y la variable 'x2'?
-La variable 'x2' representa el número de sillas que se van a producir en el negocio.
¿Cuáles son las restricciones que afectan a la producción en este ejemplo?
-Las restricciones son el tiempo disponible en el departamento de corte (120 horas) y el tiempo disponible en el departamento de ensamble (90 horas).
¿Qué contribución marginal tienen las mesas y las sillas, respectivamente?
-Las mesas aportan una contribución marginal de 50 dólares y las sillas aportan una contribución marginal de 80 dólares.
¿Qué se entiende por la 'función objetivo' en este contexto?
-La función objetivo es la ecuación que busca maximizar la ganancia, calculada como 50x1 + 80x2, donde x1 es el número de mesas y x2 es el número de sillas.
¿Cómo se expresan las restricciones en este modelo?
-Las restricciones se expresan como ecuaciones en las que la cantidad de horas de corte y ensamble para mesas y sillas no debe superar las horas disponibles: 1x1 + 2x2 ≤ 120 para corte y 1x1 + 1x2 ≤ 90 para ensamble.
¿Por qué se debe trabajar en el primer cuadrante del plano cartesiano?
-Se debe trabajar en el primer cuadrante porque no es posible producir una cantidad negativa de mesas o sillas, por lo que tanto x1 como x2 deben ser mayores o iguales a 0.
¿Cómo se obtiene la solución óptima en este modelo?
-La solución óptima se obtiene al graficar las restricciones y encontrar el punto de intersección que maximiza la ganancia, que en este caso es producir 60 mesas y 30 sillas, obteniendo una ganancia de 5,400 dólares.
¿Qué método se utiliza además del gráfico para resolver este problema?
-Además del método gráfico, se utiliza el 'método solver' en una hoja de cálculo para obtener la misma solución de manera automática y precisa.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Operations Research 03D: Linear Programming Graphical Solution Technique

Método Simplex

Intro to Simplex Method | Solve LP | Simplex Tableau

COMBINACIÓN LINEAL de Vectores en el Plano ↗️

Método Simplex - Programación Lineal
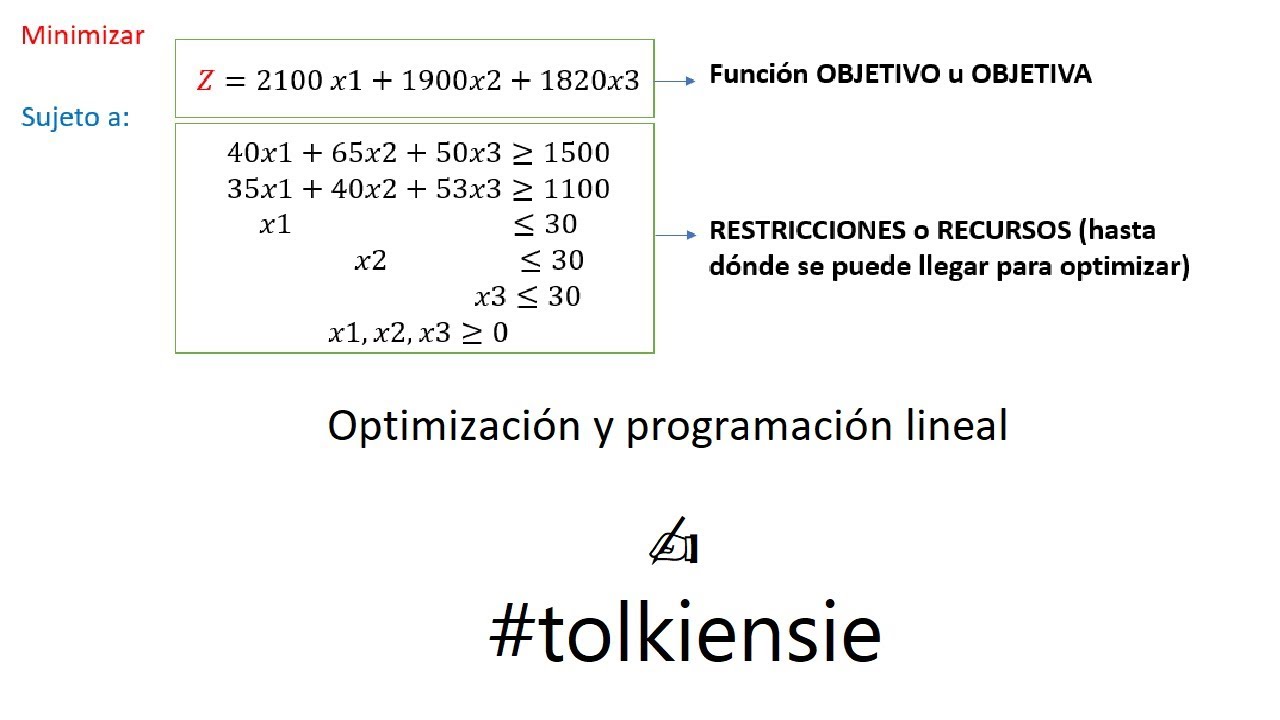
🔴PROGRAMACIÓN LINEAL partes restricciones solución método gráfico 2024 Optimización Max minimizar
5.0 / 5 (0 votes)
