Learn Merge Sort in 13 minutes 🔪
Summary
TLDRThis video script explores the Merge Sort algorithm, a divide and conquer method used in computer science for sorting arrays. It explains the recursive nature of the algorithm, dividing arrays into subarrays, and then merging them back in order. The script also covers the algorithm's time and space complexity, comparing it with other sorting methods like quick sort, heap sort, insertion sort, selection sort, and bubble sort. The video concludes with a practical demonstration of implementing Merge Sort in code.
Takeaways
- 🗡️ The Merge Sword Algorithm: The script discusses the 'Merge Sword' algorithm, which is actually the Merge Sort algorithm in computer science.
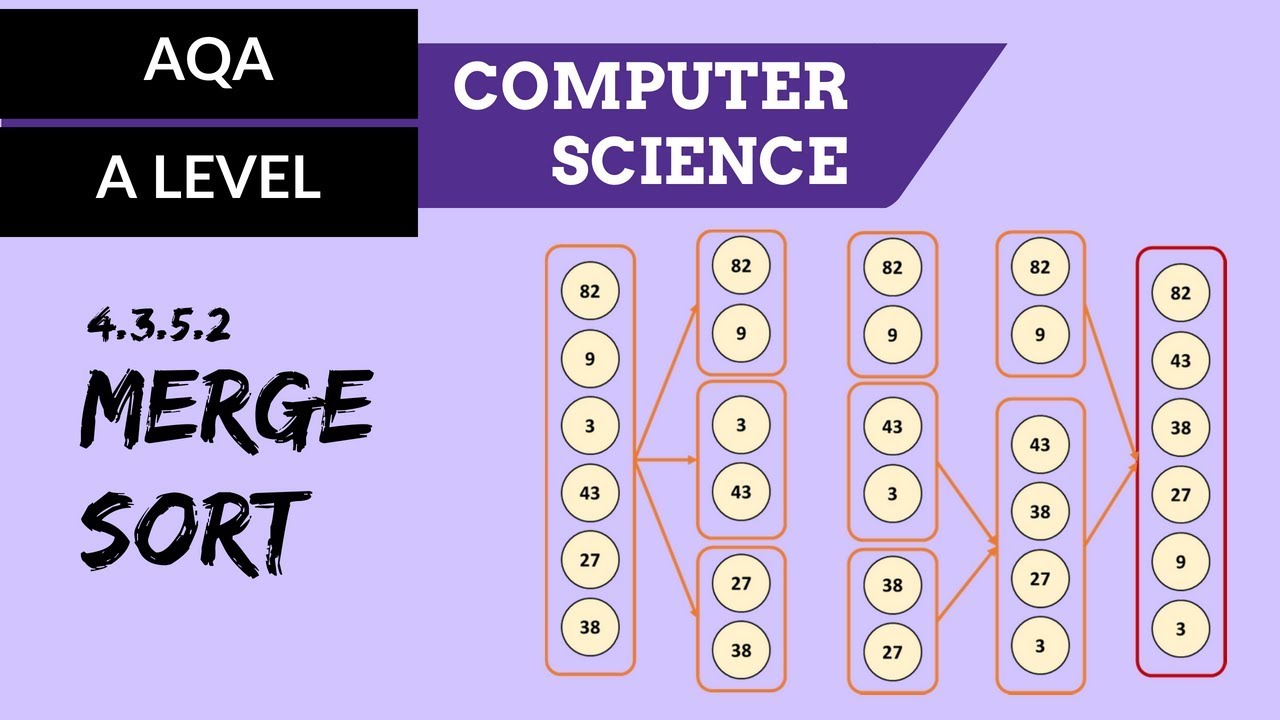
- 📚 Divide and Conquer: Merge Sort is a classic divide and conquer algorithm that divides an array into sub-arrays, sorts them, and then merges them back together.
- 🔄 Recursive Nature: The merge sort function is recursive, continually dividing the array into halves until each sub-array contains a single element.
- 📈 Base Case: The recursion stops when the sub-array size is reduced to one, which is the base case for the algorithm.
- 🔑 Helper Function: A helper function named 'merge' is used to merge the sorted sub-arrays back into the original array in sorted order.
- 🔍 Array Division: The merge sort function divides the original array into left and right sub-arrays, which are then recursively sorted.
- 🚀 Execution Strategy: In practice, merge sort executes by tackling one branch of sub-arrays at a time, starting from the leftmost branch and moving towards the right.
- ⏱️ Time Complexity: Merge Sort has a time complexity of O(n log n), making it efficient for sorting large datasets.
- 📊 Space Complexity: Unlike some other sorting algorithms, Merge Sort requires additional space for creating sub-arrays, resulting in a space complexity of O(n).
- 🛠️ Practical Implementation: The script includes a step-by-step guide on implementing the merge sort algorithm in code, including the recursive method and the merge helper method.
- 📈 Comparison with Other Sorts: Merge Sort is faster than simple sorts like insertion, selection, and bubble sort for large datasets but uses more space.
Q & A
What is the Merge Sword algorithm discussed in the video?
-The Merge Sword algorithm, likely a colloquial or mispronounced term for the Merge Sort algorithm, is a divide and conquer algorithm used in computer science for sorting arrays. It involves recursively dividing the array into two halves, sorting them, and then merging them back together in the correct order.
How does the Merge Sort algorithm work?
-Merge Sort works by dividing the array into two halves until each half has only one element, which is inherently sorted. Then, it starts merging these halves back together in a sorted manner by comparing elements and placing them in their correct positions in a new array.
What is the time complexity of the Merge Sort algorithm?
-The time complexity of the Merge Sort algorithm is O(n log n), where 'n' is the number of elements in the array. This makes it efficient for sorting large datasets.
Why is Merge Sort faster than some other sorting algorithms?
-Merge Sort is faster than algorithms like Insertion Sort, Selection Sort, and Bubble Sort when working with large datasets because of its O(n log n) time complexity, which is a quasi-linear time complexity compared to the quadratic time complexity of the other algorithms mentioned.
What is the space complexity of the Merge Sort algorithm?
-The space complexity of the Merge Sort algorithm is O(n) because it requires additional space to create subarrays during the sorting process.
How does the space usage of Merge Sort compare to other sorting algorithms?
-Merge Sort uses more space compared to Bubble Sort, Selection Sort, and Insertion Sort, which can sort in place and therefore use a constant amount of space.
What is the base case for the recursive Merge Sort function?
-The base case for the recursive Merge Sort function is when the length of the array or subarray is less than or equal to one, at which point the recursion stops because a single element is already sorted.
What is the purpose of the 'merge' helper function in Merge Sort?
-The 'merge' helper function is used to combine two sorted subarrays into a single sorted array. It takes three arguments: the left subarray, the right subarray, and the original array into which the sorted elements are merged.
How does the video script describe the process of merging in Merge Sort?
-The script describes the merging process as a series of comparisons between elements of the left and right subarrays. The smaller element is placed into the original array, and this process is repeated until all elements are merged back into the original array in sorted order.
What are the steps involved in implementing the Merge Sort algorithm as described in the video?
-The steps include: 1) Getting the length of the array and finding the middle position, 2) Creating left and right subarrays, 3) Copying elements from the original array to the subarrays, 4) Recursively calling Merge Sort on the left and right subarrays, and 5) Using the 'merge' helper function to combine the sorted subarrays back into the original array.
How does the video script illustrate the practical execution of the Merge Sort algorithm?
-The script illustrates the practical execution by describing a step-by-step process of dividing the array, recursively sorting the subarrays, and then merging them back together. It also mentions the use of a for loop to iterate over the elements and the creation of a 'merge' method to handle the merging process.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)