Learn Merge Sort in 13 minutes 🔪

Summary

This video script explores the Merge Sort algorithm, a divide and conquer method used in computer science for sorting arrays. It explains the recursive nature of the algorithm, dividing arrays into subarrays, and then merging them back in order. The script also covers the algorithm's time and space complexity, comparing it with other sorting methods like quick sort, heap sort, insertion sort, selection sort, and bubble sort. The video concludes with a practical demonstration of implementing Merge Sort in code.

Takeaways

• 🗡️ The Merge Sword Algorithm: The script discusses the 'Merge Sword' algorithm, which is actually the Merge Sort algorithm in computer science.
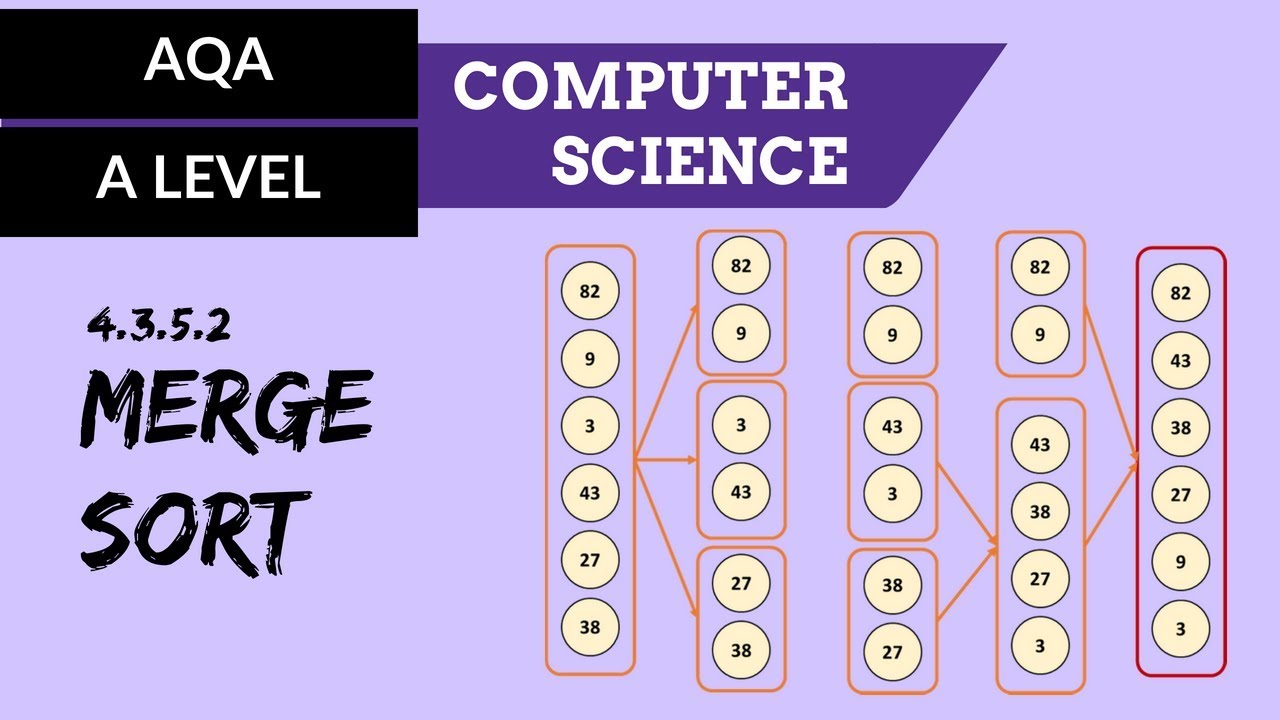
• 📚 Divide and Conquer: Merge Sort is a classic divide and conquer algorithm that divides an array into sub-arrays, sorts them, and then merges them back together.
• 🔄 Recursive Nature: The merge sort function is recursive, continually dividing the array into halves until each sub-array contains a single element.
• 📈 Base Case: The recursion stops when the sub-array size is reduced to one, which is the base case for the algorithm.
• 🔑 Helper Function: A helper function named 'merge' is used to merge the sorted sub-arrays back into the original array in sorted order.
• 🔍 Array Division: The merge sort function divides the original array into left and right sub-arrays, which are then recursively sorted.
• 🚀 Execution Strategy: In practice, merge sort executes by tackling one branch of sub-arrays at a time, starting from the leftmost branch and moving towards the right.
• ⏱️ Time Complexity: Merge Sort has a time complexity of O(n log n), making it efficient for sorting large datasets.
• 📊 Space Complexity: Unlike some other sorting algorithms, Merge Sort requires additional space for creating sub-arrays, resulting in a space complexity of O(n).
• 🛠️ Practical Implementation: The script includes a step-by-step guide on implementing the merge sort algorithm in code, including the recursive method and the merge helper method.
• 📈 Comparison with Other Sorts: Merge Sort is faster than simple sorts like insertion, selection, and bubble sort for large datasets but uses more space.

Q & A

What is the Merge Sword algorithm discussed in the video?

The Merge Sword algorithm, likely a colloquial or mispronounced term for the Merge Sort algorithm, is a divide and conquer algorithm used in computer science for sorting arrays. It involves recursively dividing the array into two halves, sorting them, and then merging them back together in the correct order.

How does the Merge Sort algorithm work?

Merge Sort works by dividing the array into two halves until each half has only one element, which is inherently sorted. Then, it starts merging these halves back together in a sorted manner by comparing elements and placing them in their correct positions in a new array.

What is the time complexity of the Merge Sort algorithm?

The time complexity of the Merge Sort algorithm is O(n log n), where 'n' is the number of elements in the array. This makes it efficient for sorting large datasets.

Why is Merge Sort faster than some other sorting algorithms?

Merge Sort is faster than algorithms like Insertion Sort, Selection Sort, and Bubble Sort when working with large datasets because of its O(n log n) time complexity, which is a quasi-linear time complexity compared to the quadratic time complexity of the other algorithms mentioned.

What is the space complexity of the Merge Sort algorithm?

The space complexity of the Merge Sort algorithm is O(n) because it requires additional space to create subarrays during the sorting process.

How does the space usage of Merge Sort compare to other sorting algorithms?

Merge Sort uses more space compared to Bubble Sort, Selection Sort, and Insertion Sort, which can sort in place and therefore use a constant amount of space.

What is the base case for the recursive Merge Sort function?

The base case for the recursive Merge Sort function is when the length of the array or subarray is less than or equal to one, at which point the recursion stops because a single element is already sorted.

What is the purpose of the 'merge' helper function in Merge Sort?

The 'merge' helper function is used to combine two sorted subarrays into a single sorted array. It takes three arguments: the left subarray, the right subarray, and the original array into which the sorted elements are merged.

How does the video script describe the process of merging in Merge Sort?

The script describes the merging process as a series of comparisons between elements of the left and right subarrays. The smaller element is placed into the original array, and this process is repeated until all elements are merged back into the original array in sorted order.

What are the steps involved in implementing the Merge Sort algorithm as described in the video?

The steps include: 1) Getting the length of the array and finding the middle position, 2) Creating left and right subarrays, 3) Copying elements from the original array to the subarrays, 4) Recursively calling Merge Sort on the left and right subarrays, and 5) Using the 'merge' helper function to combine the sorted subarrays back into the original array.

How does the video script illustrate the practical execution of the Merge Sort algorithm?

The script illustrates the practical execution by describing a step-by-step process of dividing the array, recursively sorting the subarrays, and then merging them back together. It also mentions the use of a for loop to iterate over the elements and the creation of a 'merge' method to handle the merging process.

Outlines

00:00

🤓 Introduction to Merge Sort Algorithm

This paragraph introduces the concept of the merge sort algorithm in computer science. The speaker explains that merge sort is a divide and conquer algorithm that involves passing an array to a merge sort function, which then divides the array into two sub-arrays (left and right). The process is recursive, with the function calling itself on these sub-arrays until each sub-array has only one element. The sorting and merging happen through a helper function named 'merge', which takes three arguments: the left sub-array, the right sub-array, and the original array. The merge function puts the elements back into their original array in order. The speaker also mentions that merge sort has a runtime complexity of O(n log n) and is faster than other simple sorting algorithms like insertion sort, selection sort, and bubble sort for large datasets, but it uses more space due to the creation of new sub-arrays.

05:00

💻 Implementing Merge Sort in Code

In this paragraph, the speaker dives into the practical implementation of the merge sort algorithm in code. They start by creating an array with unsorted numbers and a for loop to iterate over these elements. The merge sort method is declared as a recursive function that splits the array in half each time it is called, creating left and right sub-arrays. The base case for the recursion is when the array length is less than or equal to one. The speaker also explains how to find the middle position of the array and copy elements to the left and right sub-arrays. The recursion continues by dividing the left and right sub-arrays further until they are of size one. The merge method is then described, which involves three parameters: the left array, the right array, and the original array. The method merges the elements back into the original array in sorted order.

10:02

🔍 Detailed Explanation of the Merge Function

The final paragraph focuses on the merge function, which is crucial for the merge sort algorithm. The speaker explains that the merge function first caches the sizes of the left and right arrays in local variables. It then uses three indices to manage the original array, the left array, and the right array. The main logic of the merge function involves a while loop that continues as long as there are elements in both the left and right arrays. The function compares the elements from the left and right arrays and copies the smaller element to the original array. If one of the arrays is exhausted, the remaining elements from the other array are copied to the original array. This ensures that all elements are sorted and merged back into the original array. The speaker concludes by summarizing the merge sort algorithm, emphasizing its recursive nature, runtime complexity of O(n log n), and space complexity of O(n).

Keywords

💡Merge Sword Algorithm

The term 'Merge Sword Algorithm' seems to be a playful or colloquial name for the 'Merge Sort' algorithm discussed in the video. Merge Sort is a divide and conquer algorithm used in computer science for sorting arrays. The video script describes how this algorithm divides an array into smaller sub-arrays, sorts them, and then merges them back together. The name 'Merge Sword' adds a creative twist to the traditional algorithm name, making it more engaging for the audience.

💡Divide and Conquer

Divide and conquer is a fundamental algorithmic paradigm used in computer science, which involves breaking down a complex problem into smaller, more manageable sub-problems, solving each sub-problem recursively, and then combining their solutions. In the context of the video, the merge sort algorithm exemplifies this approach by recursively dividing the array into halves until each sub-array contains a single element, which is inherently sorted.

💡Merge Sort Function

The 'Merge Sort Function' is a specific implementation of the merge sort algorithm. It is a recursive function that takes an array as an argument, divides it into two halves, and then calls itself to sort the sub-arrays. The video script explains that this function is central to the merge sort process, as it is responsible for the recursive division of the array and the eventual sorting of its elements.

💡Sub-arrays

Sub-arrays refer to the smaller arrays created when the original array is divided during the merge sort process. In the video script, it is mentioned that the merge sort function divides the original array into two sub-arrays, which are then further divided into even smaller sub-arrays until each contains a single element. These sub-arrays are a key component of the divide and conquer strategy used in merge sort.

💡Recursive Function

A 'Recursive Function' is a function that calls itself in order to solve smaller instances of the same problem. In the script, the merge sort function is described as recursive because it continues to call itself with the sub-arrays created during the sorting process. This self-calling mechanism is crucial for the algorithm to work effectively and reach the base case where the array size is one.

💡Base Case

In the context of recursion, the 'Base Case' is the condition under which the recursive calls stop. For the merge sort algorithm discussed in the video, the base case is when the array size is reduced to one, at which point no further division is necessary because a single element is inherently sorted. The script mentions this as the stopping point for the recursive calls of the merge sort function.

💡Helper Function

A 'Helper Function' is a function that supports the main function by performing a specific task. In the video, the 'merge' function is described as a helper function for the merge sort algorithm. Its role is to take the sorted sub-arrays and merge them back together in the correct order, which is essential for the final sorted array.

💡Runtime Complexity

Runtime complexity, often expressed using 'Big O' notation, is a measure of the amount of time an algorithm takes to run as a function of the input size. The video script mentions that the merge sort algorithm has a runtime complexity of O(n log n), indicating that its execution time grows logarithmically with the size of the input, making it efficient for large datasets.

💡Space Complexity

Space complexity is a measure of the amount of memory an algorithm uses in relation to the input size. The script points out that the merge sort algorithm has a space complexity of O(n) because it requires additional space to create sub-arrays during the sorting process, unlike some other sorting algorithms that can sort in place with constant space.

💡In-Place Sorting

In-place sorting refers to sorting algorithms that do not require additional memory beyond a small, constant amount. The video script contrasts merge sort with other sorting algorithms like bubble sort, selection sort, and insertion sort, which can sort the array in place and therefore have a constant space complexity. Merge sort, on the other hand, requires additional space for sub-arrays, making it not an in-place sorting algorithm.

Highlights

Introduction to the Merge Sword (Merge Sort) algorithm in computer science.

Explanation of the divide and conquer approach used in Merge Sort.

Description of the process of dividing an array into left and right sub-arrays.

Recursive nature of the Merge Sort function and its role in array division.

The creation of a second helper function named 'merge' for sorting and merging elements.

Details on the 'merge' function's parameters and its role in ordering elements.

The practical execution of the Merge Sort function and its step-by-step breakdown.

Visualization of the sorting process through a sped-up demonstration.

Runtime complexity of the Merge Sort algorithm, O(n log n).

Comparison of Merge Sort's efficiency with other sorting algorithms.

Discussion on the space usage of Merge Sort versus in-place sorting algorithms.

Introduction to the hands-on coding portion of the video.

Coding steps to create a Merge Sort function, including array and loop setup.

Recursive method declaration for the Merge Sort algorithm.

Implementation of the base case for the recursion in the Merge Sort method.

Explanation of finding the middle position of the array and creating sub-arrays.

Process of copying elements from the original array to the left and right sub-arrays.

Recursive calls to the Merge Sort function for further array division.

Merging elements back into the original array in sorted order.

Finalization of the Merge Sort function and its space and time complexity.

Conclusion summarizing the Merge Sort algorithm's process and complexities.

Transcripts

hey what's going on everybody it's you

bro hope you're doing well and in this

video we're going to discuss

the merge sword algorithm in computer

science so

sit back relax and enjoy the show

all right what's going on people merge

sword merge sword is

a divide and conquer algorithm basically

what we do

is that we will pass an array as an

argument to a

merge sort function this function is

going to divide our array in two

we have a left array and a right array

these will be sub-arrays and we will

copy the elements over

from our original array to our two new

sub-arrays

and merge sword is a recursive function

so at the end of merge sort we will call

merge sword again and pass in our

subarrays that we create

and again the merge sort function is

going to divide our arrays in two

by creating a two new sub arrays and

then copy the elements over

and we will stop when our arrays only

have a size of one

and that's where sorting then merging

come in and with the process of merging

and sorting we will create a

second helper function named merge merge

will accept a total of three arguments

our left subarray our right subarray and

the original subarray in which

these elements came from merge is going

to take these elements

and put them back into their original

array which they came from

in order and we will do the same thing

with the next grouping of arrays

until all of these elements are merged

back into their original array in which

they came from

all in order now in practice when we do

execute this merge sort function

instead of tackling all of these

sub-arrays like one

layer at a time we will tackle them by

one branch at a time

so it's going to look a little something

like this where we will

start with the leftmost branch and then

work our way towards the right so i'll

speed up the footage and just give you a

rundown of how this works in practice

[Music]

[Music]

you

[Music]

[Music]

[Music]

[Music]

[Music]

me

[Music]

and that ladies and gentlemen is the

merge sort algorithm

the merge sort algorithm has a runtime

complexity

of big o of n log n it runs in

quasi-linear time along with quick sort

and heap sort which we still need to

talk about

so when working with large data sets

merge sort

is faster than insertion sort selection

sort and bubble sort

but on the other hand the emerge sword

algorithm uses more space

than a bubble sword selection sword and

insertion sort because we need to create

new subarrays to store elements

whereas bubble sort selection sword and

insertion sort can sort in place

so they use a constant amount of space

to do their sorting

unlike with merge sort now let's move on

to the hands-on portion of this video

and create a merge sort function in code

now

all right well let's get started we'll

need an array to work with

make up some numbers make sure that

they're not in order as well as a for

loop to iterate over the elements of our

array

so currently our array is not in order

but that's going to change soon

let's invoke a merge sort method that we

still need to declare

this is going to be a recursive method

and we will pass in an array

and each time that we invoke this method

we will split our

array in half create two sub-arrays and

then copy the elements over

so let's create and declare this method

private static void merge sort and we'll

need a helper method

too and we'll name this merge a helper

method is just a method that helps

another method basically

so private static void merge

and there's going to be three parameters

within our merge method

int left array

int right array

and int array

remember that these are arrays of

integers the first thing that we're

going to do within our merge

sort method is that we need to get the

length of our array

so let's cache that within a local

variable named length

int length equals array.length

and we'll need a base case too when do

we stop recursion

if length

is less than or equal to one then we

shall return

and this is our base case basically with

this merge sort method we're dividing

our ray in two each time if the length

is one there's no longer a need to

divide our array further

and we'll need to find the middle

position of our ray

int middle equals length divided by two

and we'll create two new sub arrays

int array left array

equals new integer array and

the size is middle and we'll create a

right array

integer array right array the size

is length minus middle

okay now we need to copy the elements of

our original array to our left and right

arrays

so we'll need two indices int i

equals zero this will be for

our left array

and int j equals

zero and this is for our right array

then let's create a for loop we don't

necessarily need to declare a new

index here we can just use i so i'm

going to add a semicolon

our condition is i is less than

length then increment

i by 1 during each iteration so our

condition

is with an if statement if i is less

than

middle then we will copy an element

from our original array to our left

array

left array at index of i

equals array at index of i

else we will copy that element

to our right array

else right array at index

of j remember that this index is for the

right array

equals array at index of i

then let's increment j by one

okay this is where recursion comes in so

outside of this for loop

we will call merge sword again

and pass in our left array

so we'll consistently divide our array

in half

we'll begin by dividing the left array

then the right array

with a separate recursive call so left

array

then right array and then call merge

so with merge we have to pass in our

left array right array

and our original array because we'll put

the elements back in order

left array right array and our original

array that we

received as an argument so that is it

for the

merge sort function let's work on merge

next first thing that we're going to do

within the merge method is cache

the size of our left array and right

array within some local variables

int left size equals

array dot length divided by 2

and right size equals

array dot length minus

left size and then we'll need

three indices int i equals zero

this is for our original array to keep

track of the position

l will be in charge of our left array

and

r will be in charge of our right array

and

these will be the indices that we're

using

okay the next part we're going to check

the conditions

for merging and we can do this with a

while loop

so our condition is going to be while l

is less than left size

and r is less than right

size so basically while there's elements

within

both our left array and right array we

will continue adding elements to our

original array

and we'll need to check to see which

element is smaller

if left array at

index of l

is less than right array

at index of r then we will copy the

element

from our left array to our original

array so we're basically comparing the

number on the left to the right

and adding whatever number is smaller

back to our original array

so array at index of i

equals left array at

index of l then we can increment i

increment l

so if the number on the left is not

smaller than the number on the right we

have to copy the element in our right

array

to our original array and we can use an

else statement else

array at index of i

equals right array at index

of our increment i increment r

so there's probably going to be one

element remaining that we cannot compare

to another element because there's only

one left

so let's write a while loop for that

condition

while l is less than left size

then we will take array at index of i

equals left array at index

of l increment i

increment l

then we'll need a another while loop if

r

is less than right size

we will copy the last right element over

array at index of i equals

right array at index of r

increment i increment r

and that should be it let's run this

and our array is now sorted in

conclusion everybody the merge sort

algorithm

recursively divides an array in two

sorts them

and then recombines them the merge sort

algorithm has a runtime complexity of

big o of n log n and a space complexity

of big o of n so that is the merge sort

algorithm

if you would like a copy of this code i

will post this to the comment section

down below

and well yeah that is the merge sword

algorithm

in computer science hey you

yeah i'm talking to you if you learned

something new then help me

help you in three easy steps by smashing

that like button

drop a comment down below and subscribe

if you'd like to become a fellow bro

[Music]

you