Ejercicio 7.77 ESTATICA - Beer & Jhonston 9na Edición - mecánica vectorial

Summary

El guion del video trata sobre el análisis estructural de una viga, incluyendo el cálculo de reacciones y el dibujo de diagramas de fuerza cortante y momento flector. Se describe el proceso de equilibrio y la conversión de una carga distribuida en una concentrada para facilitar los cálculos. Seguidamente, se explica cómo se obtienen los diagramas de fuerzas cortantes y momentos flectores, utilizando el método de las áreas. Finalmente, se determina la magnitud y la ubicación del momento flector máximo, que es un punto clave para entender la resistencia de la viga.

Takeaways

• 😀 El objetivo es calcular las reacciones en una viga y las cargas mostradas en las figuras.
• 🔍 Se identifican dos componentes de la reacción en el apoyo A: una vertical (Ay) y una horizontal (Ax).
• 📐 Se utiliza la ecuación de equilibrio de momentos alrededor del apoyo A para calcular las reacciones.
• 📏 Se convierte la carga distribuida en una carga concentrada para facilitar el cálculo de reacciones.
• 📐 El área de la carga distribuida rectangular es 19.2 kN, ubicada en su centroide a 1.2 m.
• 🔢 Se determina la reacción normal B sub y (By) usando la relación de momentos y la distancia del centroide a 2 m.
• 🚫 La componente horizontal de la reacción en A (Ax) es cero debido a la ausencia de cargas externas en el eje X.
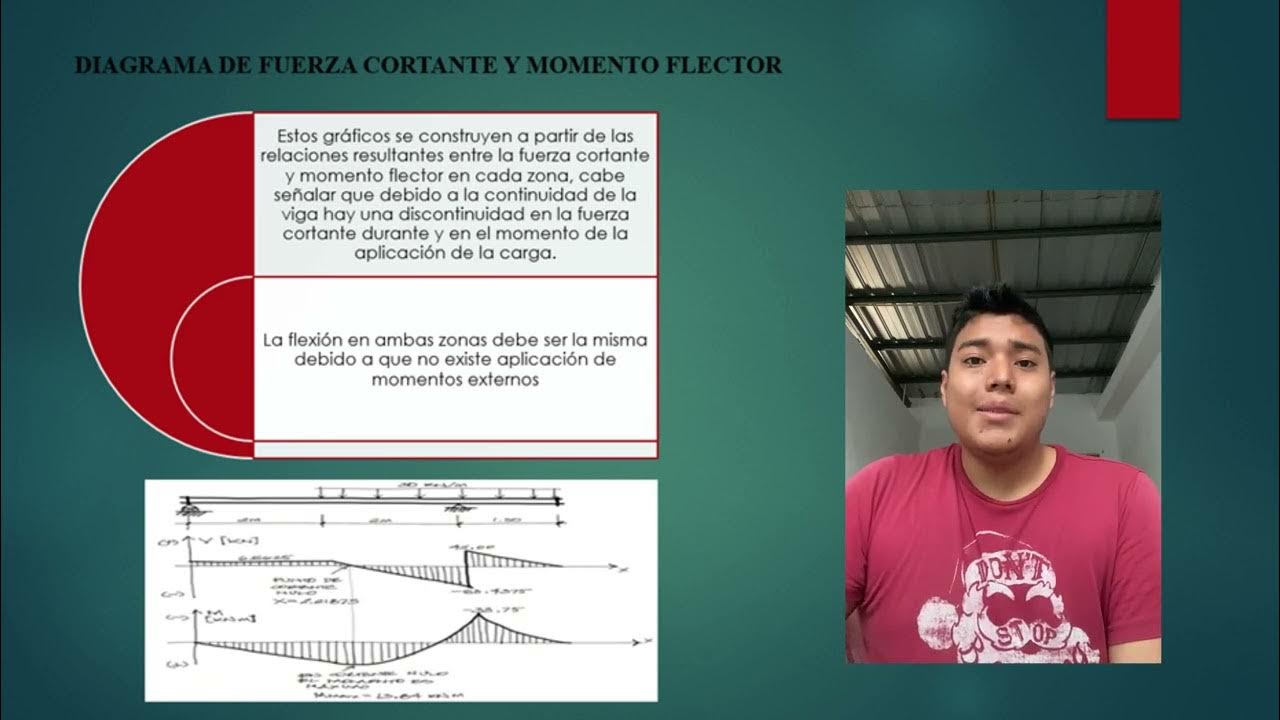
• 📉 El diagrama de fuerza cortante muestra una carga inicial de 7.2 kN y luego una carga distribuida que disminuye hasta -12 kN.
• 📊 El diagrama de momento flector se construye a partir de las áreas bajo la curva de la fuerza cortante.
• 📍 El momento flector máximo se alcanza con un valor de 9 kN·m, ubicado a 2 m del extremo izquierdo de la viga.
• 📝 El método de las áreas se utiliza para calcular el diagrama de momentos flectores, considerando áreas rectangulares y triangulares.

Q & A

¿Qué es lo primero que se debe hacer para resolver el ejercicio de la viga?

Lo primero que se debe hacer es calcular las reacciones en soporte A y B, que incluyen componentes verticales y horizontales.

¿Cuál es la ecuación de equilibrio utilizada para calcular las reacciones en el soporte A?

Se utiliza la ecuación de momentos alrededor del soporte A, donde se suman los momentos positivos generados por las cargas y se iguala a cero para encontrar las reacciones.

¿Cómo se convierte una carga distribuida en una carga concentrada para el cálculo de reacciones?

Se determina el área que genera la carga distribuida, que en este caso es un rectángulo con base y altura, y se multiplica para obtener la carga concentrada equivalente.

¿Dónde se ubica la carga concentrada una vez que se ha calculado?

La carga concentrada se ubica en el centroide de la distribución, que para una forma rectangular es la mitad de la base.

¿Cuál es el valor de la carga concentrada y su ubicación en el script?

La carga concentrada es de 19.2 kN y está ubicada a 1.2 m del soporte A.

¿Cómo se determina la magnitud de la reacción horizontal B_sub_x?

Se determina a través de la ecuación de sumatoria de fuerzas en x, resultando que B_sub_x es igual a cero ya que no hay cargas externas en x.

¿Cómo se calcula el momento flector máximo en el script?

Se calcula utilizando el diagrama de momentos flectores, que se construye a partir de las áreas bajo la curva de la fuerza cortante.

¿Qué método se utiliza para dibujar el diagrama de fuerzas cortantes?

Se utiliza el método de las áreas, donde se integran las fuerzas cortantes para obtener el diagrama de momentos flectores.

¿Cuál es la magnitud y la ubicación del momento flector máximo según el script?

El momento flector máximo es de 9 kN·m y se encuentra a una distancia de 2 m desde el extremo izquierdo de la viga.

¿Cómo se determina la pendiente del momento flector en el diagrama?

La pendiente del momento flector se determina a partir de la fuerza cortante, que es la derivada de la carga en el punto de interés.

¿Qué significa el resultado del momento flector cuando se cruzan las curvas en el diagrama?

Cuando las curvas se cruzan en el diagrama de momentos flectores, indica un cambio en la dirección de la curvatura de la viga, lo que puede ser crítico para el diseño estructural.