Menentukan Nilai Trigonometri Segitiga Siku Siku Perbandingan Trigonometri segitiga Siku Siku

Summary

This tutorial explains basic trigonometry concepts, focusing on sine, cosine, and tangent ratios in right-angled triangles. It covers two examples where the Pythagorean theorem is used to find missing side lengths, followed by calculating the trigonometric ratios. The first example explores sine and cosine for angle A in a triangle with sides 3 and 2, while the second demonstrates tangent and sine for angle B in a triangle with a hypotenuse of 5 and a side of 4. The video emphasizes the importance of knowing side lengths and applying the Pythagorean theorem to solve trigonometric problems effectively.

Takeaways

• 😀 The tutorial covers basic trigonometry, specifically focusing on the ratios of the sides of a right triangle.
• 😀 The first example involves a right triangle with sides of lengths 3 and 2, where the task is to find the sine and cosine of angle A.
• 😀 The Pythagorean theorem is essential in solving for the missing hypotenuse (denoted as X) in right triangles.
• 😀 The hypotenuse for the first triangle is found using the formula X = √(3² + 2²), resulting in X = √13.
• 😀 The sine of angle A (Sin A) is calculated as the ratio of the opposite side (2) to the hypotenuse (√13), and is simplified to 2/√13.
• 😀 The cosine of angle A (Cos A) is calculated as the ratio of the adjacent side (3) to the hypotenuse (√13), and is simplified to 3/√13.
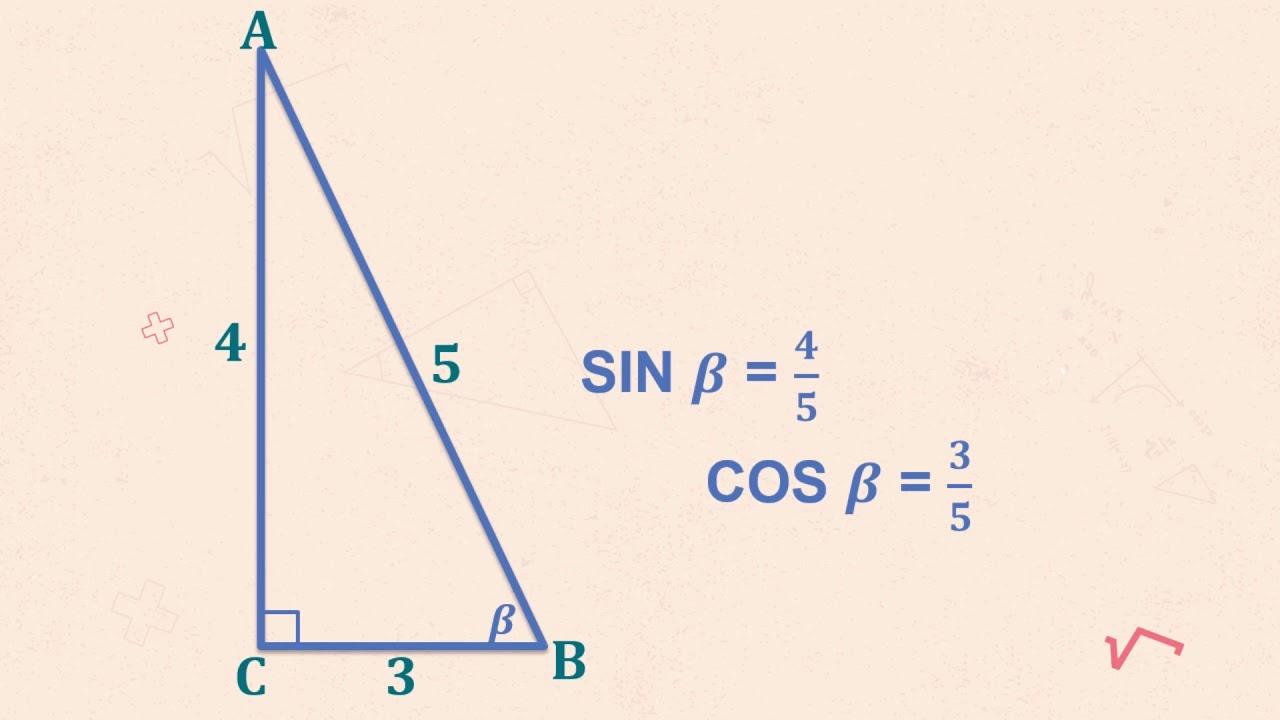
• 😀 The second example deals with a right triangle where the hypotenuse is 5 and one leg is 4, and asks to find the tangent and sine of angle B.
• 😀 The missing side (Y) of the triangle is found using the Pythagorean theorem, Y = √(5² - 4²), resulting in Y = 3.
• 😀 The tangent of angle B (Tan B) is calculated as the ratio of the opposite side (3) to the adjacent side (4), giving a value of 3/4.
• 😀 The sine of angle B (Sin B) is calculated as the ratio of the opposite side (3) to the hypotenuse (5), resulting in a value of 3/5.

Q & A

What is the main topic of the tutorial in the video?

The main topic of the tutorial is basic trigonometry, specifically dealing with ratios of sides in right-angled triangles.

How do you calculate the hypotenuse in a right-angled triangle?

The hypotenuse can be calculated using the Pythagorean theorem, which states that the square of the hypotenuse (X) is equal to the sum of the squares of the two other sides. In the example, the hypotenuse was calculated as the square root of 3² + 2², resulting in √13.

What is the formula for sine (sin) in trigonometry?

The formula for sine is the ratio of the opposite side to the hypotenuse in a right-angled triangle. In the given example, sin(A) is calculated as 2/√13, which is rationalized to 2/(13√13).

How do you calculate cosine (cos) in trigonometry?

Cosine is the ratio of the adjacent side to the hypotenuse. In the example, cos(A) is calculated as 3/√13, which is then rationalized to 3/(13√13).

What is the formula for tangent (tan) in trigonometry?

Tangent is the ratio of the opposite side to the adjacent side in a right-angled triangle. In the second example, tan(B) is 3/4.

What method is used to calculate missing side lengths in a right-angled triangle?

The missing side length is calculated using the Pythagorean theorem. In the second example, the side length was calculated by subtracting the square of the known side from the square of the hypotenuse.

What is the value of sin(A) in the first example?

In the first example, sin(A) is calculated as 2/√13, which is rationalized to 2/(13√13).

What is the value of cos(A) in the first example?

In the first example, cos(A) is calculated as 3/√13, which is rationalized to 3/(13√13).

Why is rationalization used in trigonometric calculations?

Rationalization is used to remove square roots from the denominator to make the expression more manageable and easier to interpret mathematically.

What was the value of the missing side length (y) in the second example, and how was it calculated?

The missing side length (y) was calculated using the Pythagorean theorem. Given the hypotenuse was 5 and one side was 4, the missing side was found as the square root of 5² - 4², which equals 3.