Deriving the Heat Equation: A Parabolic Partial Differential Equation for Heat Energy Conservation

Summary

This video dives into the derivation of the one-dimensional heat equation, a key concept in thermal physics. The speaker begins by explaining the physical principles behind heat transfer, including conservation of thermal energy and Fourier's law of heat conduction. The heat equation is then formulated as a partial differential equation that models how temperature evolves over time in a material. The speaker also touches on boundary conditions and the role of external heat sources. This foundational explanation sets the stage for exploring more complex, multidimensional heat transfer problems.

Takeaways

• 😀 The process begins by explaining how to derive the one-dimensional heat equation from basic physical principles.
• 😀 The conservation of thermal energy is a key concept in understanding heat transfer in the rod.
• 😀 Heat flux is introduced as a fundamental aspect of heat conduction, described by Fourier's law.
• 😀 Fourier’s law states that heat flux is proportional to the temperature gradient across the material.
• 😀 The heat equation is derived by balancing the rate of heat change in a segment with the heat flux through its boundaries.
• 😀 The equation for heat flux is written as q(x,t) = -κ ∂u/∂x, where κ is the thermal conductivity.
• 😀 The one-dimensional heat equation incorporates terms for heat flux and internal heat generation.
• 😀 A simplified version of the heat equation appears when material properties (thermal conductivity, density, and specific heat) are constant.
• 😀 The heat equation is expressed as ∂u/∂t = α² ∂²u/∂x² + q(x,t)/(ρc) where α² = κ/(ρc) is the thermal diffusivity.
• 😀 The derivation leads to a partial differential equation that models the temperature evolution in a spatially extended material.
• 😀 The resulting equation serves as a foundation for more advanced models, including higher-dimensional heat equations and steady-state solutions.

Q & A

What is the main objective of deriving the one-dimensional heat equation?

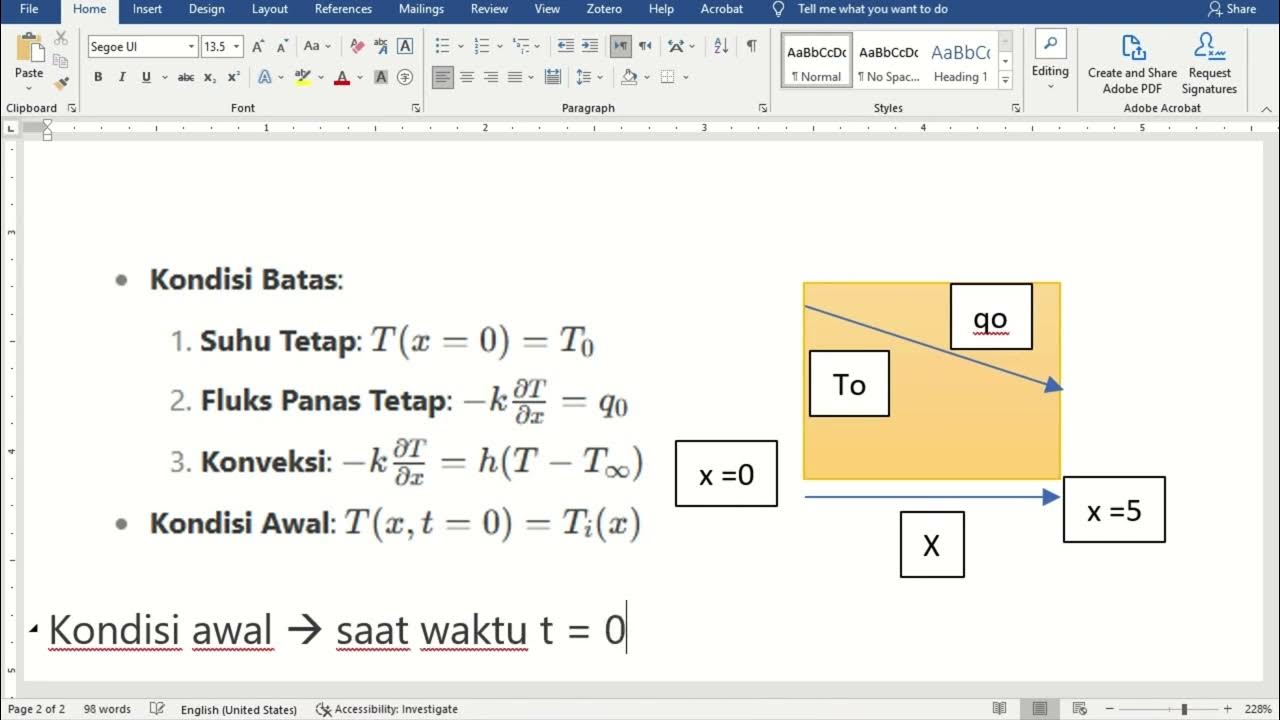
The main objective is to derive a partial differential equation (PDE) that represents the conservation of thermal energy in a thin metal rod. This equation will describe how temperature evolves over time and space due to heat conduction and potential heat generation or loss.

What are the key assumptions made in the script for deriving the heat equation?

The key assumptions include an insulated rod, fixed boundary conditions at both ends of the rod, and an initial temperature distribution. These assumptions simplify the process by removing external heat loss or gain through radiation.

How does the conservation of thermal energy relate to the heat equation?

The conservation of thermal energy states that the rate of change of heat energy in the system equals the heat flux through boundaries and any heat generated or lost at points in space. This relationship is mathematically expressed through the heat equation.

What role does Fourier's law of heat conduction play in the derivation of the heat equation?

Fourier's law of heat conduction is crucial because it links the heat flux to the temperature gradient. It states that heat flux is proportional to the negative gradient of temperature, which is central to deriving the mathematical form of the heat equation.

What does the term 'heat flux' refer to in the script?

Heat flux refers to the rate at which heat energy flows through a material. It is related to the temperature gradient and indicates whether heat is moving into or out of a given segment of the rod.

Why is the negative sign in the Fourier heat flux equation important?

The negative sign in Fourier's law indicates that heat flows from regions of higher temperature to regions of lower temperature. This aligns with the physical expectation that heat naturally moves towards cooler areas.

What does the term 'source term' in the heat equation represent?

The source term represents external heat sources or sinks, such as heat generated by atomic processes, radiation, or mechanical heating methods like a blowtorch. It accounts for any local addition or removal of heat in the system.

What simplification was made regarding the material properties in the derivation of the heat equation?

The material properties, such as thermal conductivity (kappa), density (rho), and specific heat (c), were assumed to be constant. This simplification makes the resulting equation more manageable but can be adjusted for materials where these properties vary with position.

What is the final form of the heat equation for a constant material in the script?

The final form of the heat equation for a constant material is: ∂u/∂t = (κ / (c * ρ)) * ∂²u / ∂x² + q(x,t), where u(x,t) is the temperature, κ is the thermal conductivity, c is the specific heat, ρ is the density, and q(x,t) represents the source term.

How is the heat equation generalized for multi-dimensional systems, as mentioned in the script?

For multi-dimensional systems, such as 2D or 3D objects, the heat equation involves the Laplacian of the temperature field instead of the second spatial derivative. This generalization accounts for heat diffusion in multiple directions and forms the basis for solving more complex thermal problems.