LECTURE NOTES: HEAT TRANSFER, CHAPTER II, PART 2
Summary
TLDRThe transcript delves into the principles of heat conduction, focusing on one-dimensional cases across various geometries, including flat walls, cylinders, and spheres. It explains the derivation of heat conduction equations in Cartesian, cylindrical, and spherical coordinates, highlighting the assumptions made for simplifying the problems. The content also covers multidimensional heat conduction, boundary conditions, and internal heat generation, emphasizing their significance in solving real-world thermal problems. The presentation concludes with a discussion on boundary and interface conditions essential for determining temperature distributions and heat flux in different materials.
Takeaways
- 😀 Heat conduction in cases like glasshouse walls, metal plates, steam pipes, and nuclear fuel elements can often be approximated as one-dimensional.
- 😀 In one-dimensional heat conduction, the heat flow occurs predominantly in one direction, with other directions often neglected.
- 😀 The general equation for one-dimensional heat conduction can be derived in Cartesian, cylindrical, and spherical coordinates.
- 😀 Heat conduction equations are derived by applying energy balance to a thin element in a medium, leading to an equation for heat transfer rates and temperature changes.
- 😀 The one-dimensional heat conduction equation can have various forms depending on factors like heat conductivity, steady vs. transient heat transfer, and heat generation.
- 😀 In cylindrical and spherical coordinates, the direction of heat transfer is radial, with the cross-sectional area being represented by the surface area of the cylinder or sphere.
- 😀 Most practical cases of heat transfer can be approximated as one-dimensional, but in some cases, multidimensional heat transfer must be considered.
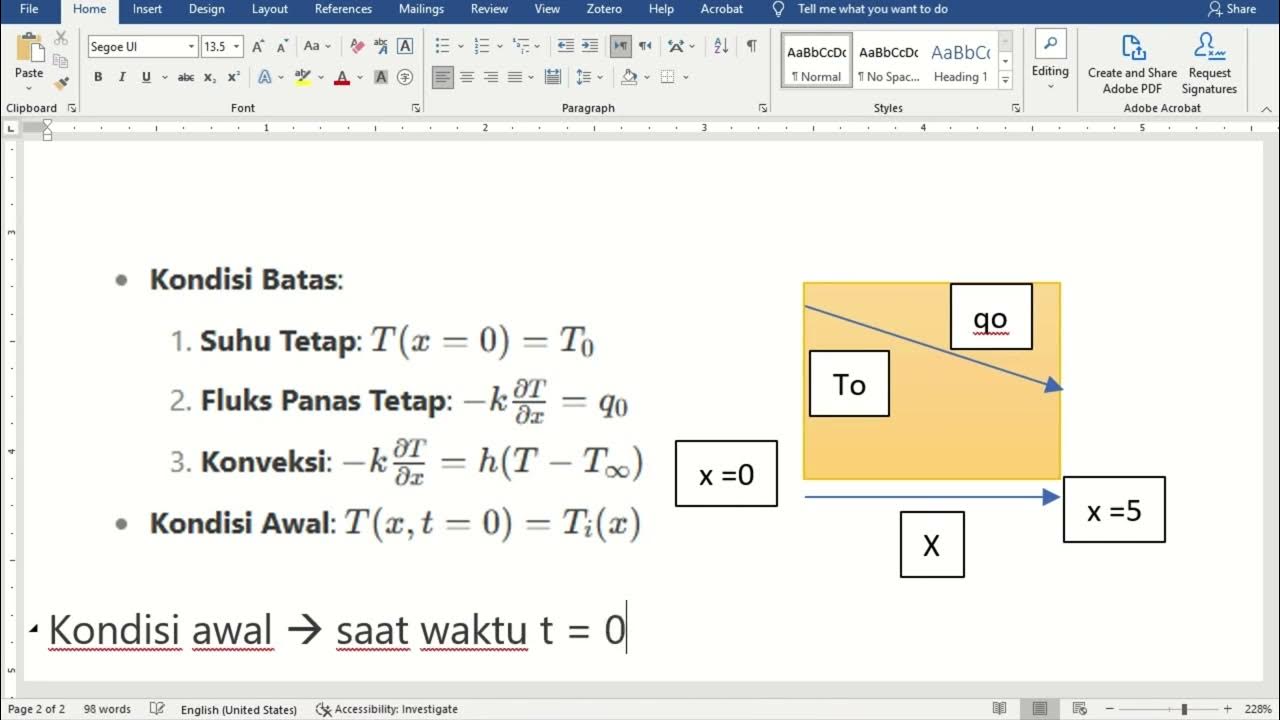
- 😀 To solve heat conduction equations, boundary conditions must be defined since the differential equation alone does not specify unique solutions.
- 😀 Different boundary conditions include fixed temperature, fixed heat flux, convection, radiation, and conditions at the interface of two materials with different properties.
- 😀 Heat generation in a medium is represented by a source term, often denoted as 'e_gen', and is crucial for cases where energy is converted into heat, such as electrical, chemical, or nuclear reactions.
- 😀 Boundary conditions for heat conduction problems involve specifying conditions on the surface, including temperature or heat flux, and in cases with internal heat generation, the relationship between surface temperature, environmental temperature, and heat transfer is crucial.
Q & A
What is the main focus of the discussion in the provided transcript?
-The main focus of the discussion is on the concept of heat conduction, specifically one-dimensional heat conduction in different geometries such as Cartesian, cylindrical, and spherical coordinates. It also covers how to derive and apply the heat conduction equation in various scenarios.
What assumption is made for one-dimensional heat conduction in most cases?
-In most cases, it is assumed that heat conduction is dominant in one direction and negligible in other directions. This simplifies the problem to a one-dimensional heat conduction equation.
How is the heat conduction equation derived for one-dimensional cases in Cartesian coordinates?
-The heat conduction equation for one-dimensional cases in Cartesian coordinates is derived by considering an infinitesimal element within a large flat wall. The energy balance on this element is expressed in terms of the heat flux entering and leaving the element, as well as internal heat generation and energy change over time. The resulting equation is then simplified and taken to the limit as the element size approaches zero.
What are the conditions under which the heat conduction equation simplifies further?
-The equation simplifies further in cases where the thermal conductivity is constant, there is steady-state heat transfer, or there is no internal heat generation. Additionally, the equation can also simplify under transient conditions or in cases with varying thermal conductivity.
What are the differences between the heat conduction equations in Cartesian, cylindrical, and spherical coordinates?
-The primary difference lies in the direction of heat transfer and the geometry of the heat flow. In Cartesian coordinates, heat transfer occurs in one direction with a flat cross-section. In cylindrical coordinates, the heat transfer is radial with the cross-sectional area represented by the surface of a cylinder. In spherical coordinates, heat transfer also occurs radially, with the cross-section represented by a spherical shell.
What does 'multidimensional heat conduction' refer to, and how is it handled mathematically?
-Multidimensional heat conduction refers to cases where heat transfer occurs in more than one direction, requiring consideration of multiple spatial variables. It is handled mathematically by extending the one-dimensional heat conduction equation into higher dimensions, resulting in a more complex set of equations that account for heat transfer in all relevant directions.
How are boundary conditions essential in solving heat conduction equations?
-Boundary conditions are essential in solving heat conduction equations because they define the temperature or heat flux at the boundaries of the system. Without boundary conditions, the solution to the heat conduction equation would be incomplete and unable to match physical reality. For one-dimensional problems, two boundary conditions are required, while more complex cases may require more boundary conditions.
What are some examples of boundary conditions used in heat conduction problems?
-Examples of boundary conditions in heat conduction problems include fixed temperature (Dirichlet boundary condition), fixed heat flux (Neumann boundary condition), convective heat transfer at the surface, radiative heat exchange, and interface conditions between two different materials.
What is 'internal heat generation' and how is it incorporated into the heat conduction equation?
-Internal heat generation refers to the generation of heat within the material itself, such as from electrical heating, chemical reactions, or nuclear reactions. It is incorporated into the heat conduction equation as a source term (e.g., 'e do gen'), which represents the rate of heat generation per unit volume.
Why are the concepts of surface temperature and maximum temperature important in heat conduction with internal heat generation?
-Surface temperature and maximum temperature are important because they determine the thermal performance of the material, such as its efficiency in transferring heat. For steady-state conditions, the surface temperature can be calculated by balancing the heat generation rate with convective heat transfer, while the maximum temperature is critical in assessing material limitations and potential damage.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Persamaan transfer kalor konduksi steady state satu dimensi

Deriving the Heat Equation: A Parabolic Partial Differential Equation for Heat Energy Conservation
MATERI BANGUN DATAR DAN RUANG

Year 7 Maths | 3D Solids Prisms Pyramids

9. Fenomena Transport - Termodinamika - Fisika N20

Luas Permukaan Prisma dan Tabung Hal 213-215 Bab 6 Kelas 7 Kurikulum Merdeka
5.0 / 5 (0 votes)