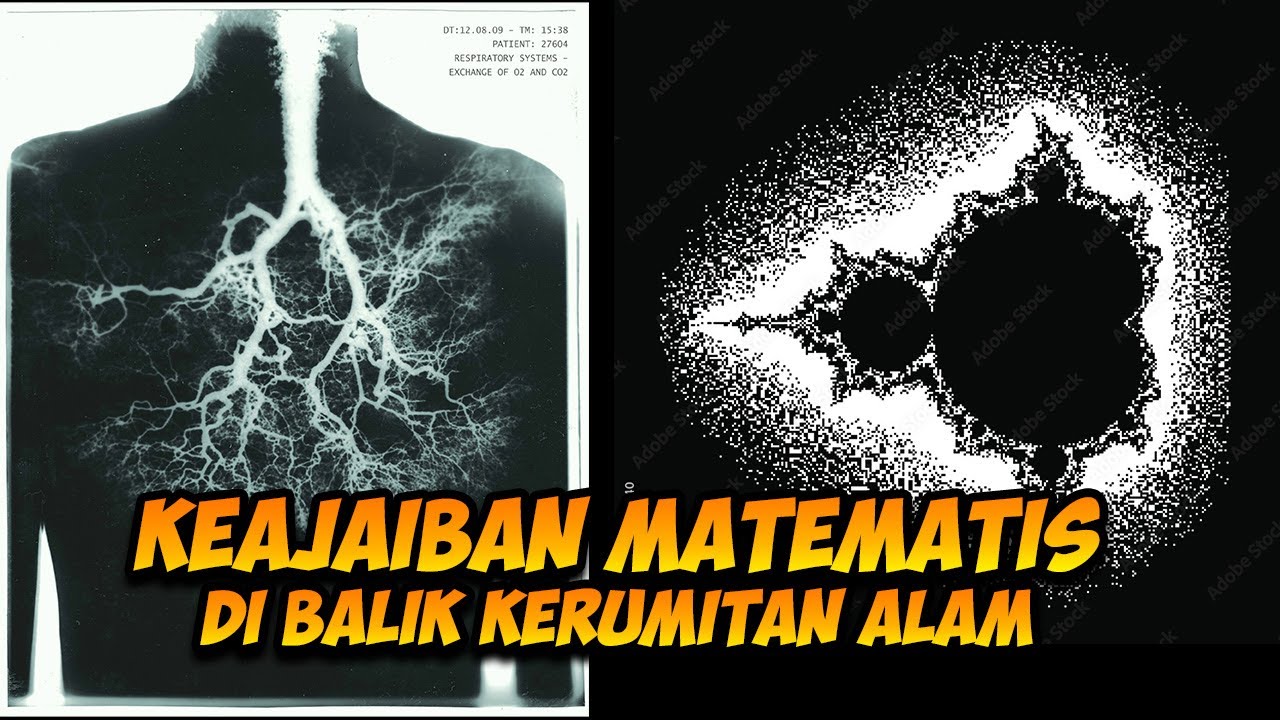
Fractals are typically not self-similar

Summary

This video delves into the fascinating world of fractals and fractional dimensions, explaining how these intricate shapes arise in nature and mathematics. By exploring self-similar structures like the Sierpinski triangle and Von Koch curve, the script demonstrates how fractals are defined by their roughness, rather than perfect self-similarity. It introduces the concept of fractional dimensions, showing how they quantify the complexity of shapes such as coastlines, which exhibit roughness at every zoom level. Ultimately, the video highlights how fractal geometry offers a more realistic way to model natural forms, offering new insights into the world around us.

Takeaways

• 😀 Fractals are shapes that exhibit infinite complexity and repetition, often admired by programmers for their simplicity in code and intricate results.
• 😀 A common misconception is that fractals are only self-similar shapes, but they actually represent roughness and irregularity, as seen in natural phenomena.
• 😀 Benoit Mandelbrot, the father of fractal geometry, focused on using fractals to model nature, counteracting the idealized smoothness of calculus.
• 😀 True fractals are defined by a fractional dimension, which can be any positive real number, not just whole numbers.
• 😀 Shapes like the Sierpinski triangle and Von Koch snowflake are often used as examples of fractals, though they are based on self-similar patterns.
• 😀 Fractal dimension quantifies how a shape's 'mass' changes as it is scaled, with mass decreasing based on the scaling factor raised to the power of the shape’s dimension.
• 😀 Self-similar fractals like the Sierpinski triangle can have fractional dimensions, such as 1.585D, which means their mass doesn’t scale neatly like integer dimensions.
• 😀 The Von Koch curve, another self-similar fractal, has a dimension of approximately 1.262D, demonstrating how fractional dimensions reflect more complex shapes.
• 😀 Traditional geometric shapes like lines, squares, and cubes follow integer dimensions (1D, 2D, 3D), where mass scales in predictable integer powers of a factor.
• 😀 Fractal dimension helps explain roughness in real-world shapes, such as the coastline of Britain, which has a dimension of 1.21D, indicating its jagged nature at multiple scales.

Q & A

What is the common misconception about fractals?

The common misconception is that fractals are shapes that are perfectly self-similar, meaning they look exactly the same when zoomed in at any level.

How did Benoit Mandelbrot define fractals differently from the popular misconception?

Mandelbrot defined fractals as shapes that capture roughness and irregularity, with a fractal dimension that is not necessarily an integer. He emphasized modeling nature's complexity rather than focusing solely on self-similarity.

What is the key concept behind fractal dimension?

Fractal dimension refers to the way a shape's 'mass' or 'size' changes as it is scaled, and it can be a fractional value rather than an integer. This helps describe irregular and rough shapes in nature.

Why is fractal dimension important for modeling the real world?

Fractal dimension allows us to model the roughness of real-world objects like coastlines or terrain, which do not follow smooth, idealized patterns but instead exhibit complex, self-similar behavior at different scales.

What is the fractal dimension of the Sierpinski triangle?

The Sierpinski triangle has a fractal dimension of approximately 1.585, which means it is not exactly one-dimensional or two-dimensional but instead has a fractional dimension.

How is the fractal dimension of the Von Koch curve determined?

The fractal dimension of the Von Koch curve is determined by the scaling factor. With a scaling factor of one-third, the dimension is approximately 1.262, calculated by using logarithms to solve for the power in the scaling equation.

What challenges are there when assigning a fractal dimension to shapes?

Assigning a fractal dimension can be tricky because it depends on the level of zoom and the method used to measure the shape. The dimension can change based on the scale, so the correct value is often determined by analyzing the shape at multiple zoom levels.

How is the fractal dimension of irregular, non-self-similar shapes like coastlines determined?

For non-self-similar shapes like coastlines, the fractal dimension is determined empirically by counting the number of grid squares that touch the shape at different scales and then using logarithms to find a linear relationship that reveals the dimension.

How does the concept of fractal dimension apply to natural objects like coastlines?

In natural objects like coastlines, fractal dimension helps quantify their roughness. For instance, the coastline of Britain has a fractal dimension of approximately 1.21, meaning it has a jaggedness that remains consistent across different scales.

What makes fractals in nature different from man-made objects in terms of dimension?

Fractals in nature tend to have a fractional dimension that quantifies their roughness, while man-made objects usually have integer dimensions, reflecting their smooth and uniform surfaces as opposed to nature's irregular patterns.