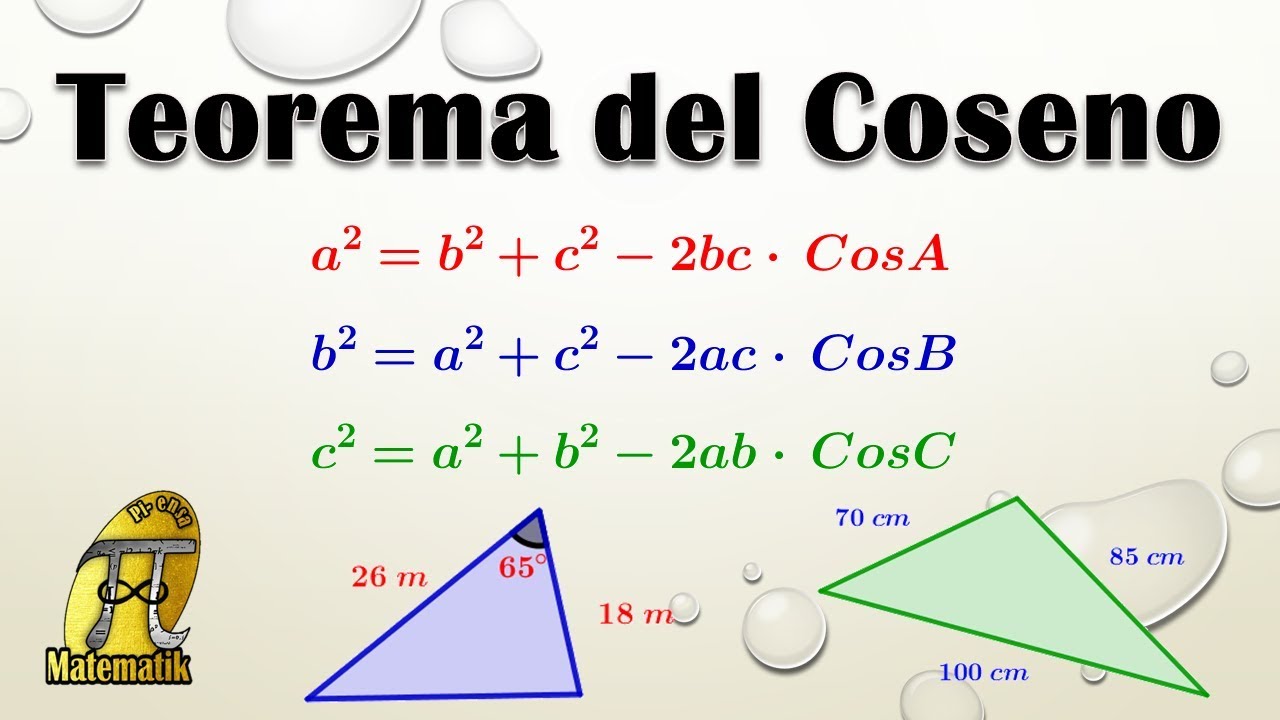
Cómo y cuándo usar el Teorema del Seno - Parte 2
Summary
TLDREn este video, el presentador explica cómo aplicar el teorema del seno para resolver triángulos, enfocándose en un caso donde se conocen dos ángulos y un lado. A través de un ejemplo detallado, muestra cómo calcular los lados faltantes utilizando las relaciones trigonométricas. Primero, se calcula el ángulo faltante y luego se aplica la ley de los senos para encontrar los otros dos lados. Además, el video destaca la importancia de verificar los resultados observando la relación entre los ángulos y los lados opuestos. Se promete continuar con una explicación sobre el teorema del coseno en futuros videos.
Takeaways
- 😀 El teorema del seno se aplica cuando tenemos dos ángulos y un lado en un triángulo.
- 😀 Si se nos dan dos ángulos y un lado, podemos encontrar el tercer ángulo usando la suma de 180 grados.
- 😀 El ángulo faltante se puede encontrar fácilmente restando la suma de los dos ángulos dados de 180 grados.
- 😀 Una vez que tenemos los tres ángulos, podemos usar el teorema del seno para encontrar los lados faltantes.
- 😀 El teorema del seno establece que la relación entre un lado y el seno de su ángulo opuesto es constante en un triángulo.
- 😀 Se puede usar la regla de tres directa para despejar los lados desconocidos del triángulo cuando se tiene la información de un lado y sus ángulos opuestos.
- 😀 Para resolver el ejercicio, se debe calcular el seno de los ángulos dados y aplicar la fórmula adecuada para encontrar los lados.
- 😀 El valor de un lado mayor siempre debe corresponder al ángulo mayor, lo que sirve como verificación de los resultados.
- 😀 En este ejemplo, se resolvieron dos lados desconocidos usando el teorema del seno y la información proporcionada.
- 😀 Al aplicar correctamente el teorema del seno, encontramos los lados con precisión y coherencia respecto a los ángulos.
- 😀 El video concluye con la explicación de cómo usar el teorema del seno en situaciones de triángulos con dos ángulos y un lado, y anticipa el tema del teorema del coseno para el siguiente video.
Q & A
¿En qué consiste el Teorema del Seno?
-El Teorema del Seno establece que, en un triángulo cualquiera, las razones entre el largo de un lado y el seno del ángulo opuesto a ese lado son constantes. Es decir, a/sen(A) = b/sen(B) = c/sen(C).
¿Cuándo se puede aplicar el Teorema del Seno?
-El Teorema del Seno se puede aplicar cuando se tiene un triángulo con dos ángulos y un lado, o bien con dos lados y un ángulo no comprendido. En este caso, se puede encontrar el valor de los lados o de los ángulos faltantes.
¿Qué información nos dan en el segundo ejemplo del video?
-En el segundo ejemplo se nos da un triángulo con los lados 'a' y 'b', el ángulo 'A' de 35 grados, el ángulo 'B' de 65 grados, y el lado 'c' de 98 centímetros. A partir de esta información, se deben calcular los lados 'a' y 'b'.
¿Cómo se calcula el ángulo faltante cuando nos dan dos ángulos?
-Se calcula restando la suma de los dos ángulos dados de 180 grados, ya que la suma de los ángulos internos de un triángulo siempre es 180 grados. En este caso, 180 - 35 - 65 = 80 grados.
¿Por qué se dice que, al tener dos ángulos, realmente tenemos tres ángulos?
-Porque la suma de los tres ángulos internos de cualquier triángulo siempre es 180 grados. Si tenemos dos ángulos, el tercero se puede calcular restando la suma de los dos ángulos dados de 180 grados.
¿Qué relación se usa para resolver el triángulo en el video?
-Se utiliza la relación entre los lados y los senos de los ángulos, es decir, la fórmula del Teorema del Seno: (lado c / sen(ángulo C)) = (lado a / sen(ángulo A)).
¿Cómo se despeja el valor del lado 'a' en la fórmula?
-Para despejar 'a', se usa una regla de tres directa. Se multiplica el valor del lado 'c' por el seno del ángulo 'A' y se divide entre el seno del ángulo 'C'.
¿Qué resultado se obtiene para el lado 'a' en el ejemplo?
-El valor de 'a' es 57.07 centímetros, que es el resultado obtenido al aplicar la regla de tres y utilizar los valores correspondientes.
¿Qué método se utiliza para calcular el lado 'b' en el video?
-Se utiliza el mismo proceso que para calcular el lado 'a'. Se aplica la relación entre los lados y los senos de los ángulos, pero con los valores correspondientes para el ángulo 'B'.
¿Cómo se verifica que los resultados sean coherentes?
-Se verifica que el ángulo más grande corresponde al lado más largo, y el ángulo más pequeño corresponde al lado más corto. Si esta relación no se cumple, significa que hay un error en los cálculos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)