Razones trigonométricas de un ángulo | Ejemplo 1
Summary
TLDREn este video, el instructor ofrece una introducción a las razones trigonométricas de un ángulo, utilizando como ejemplo el ángulo teta. Se explica que las razones trigonométricas son el resultado de operaciones geométricas en un triángulo rectángulo, como el seno (cateto opuesto sobre hipotenusa), el coseno (cateto adyacente sobre hipotenusa) y la tangente (cateto opuesto sobre cateto adyacente). A lo largo del video, se identifica a cada lado del triángulo y se calculan las razones trigonométricas correspondientes, como el seno de teta (3/5), el coseno de teta (4/5) y la tangente de teta (3/4), entre otras. Además, se menciona que en futuras lecciones se abordará cómo encontrar el valor del ángulo cuando uno de los lados es desconocido. El video concluye con un ejercicio para que los estudiantes practiquen y un recordatorio de que las razones trigonométricas pueden expresarse tanto en forma de fracción como en decimal. El instructor anima a los espectadores a suscribirse, comentar y compartir el contenido para profundizar en el tema.
Takeaways
- 📐 Los trigonogramas son funciones que relacionan los ángulos de un triángulo rectángulo con las relaciones entre sus lados.
- 📏 El seno de un ángulo (teta) se define como la relación entre el cateto opuesto y la hipotenusa.
- 📏 El coseno de un ángulo (teta) es la relación entre el cateto adyacente y la hipotenusa.
- 📏 La tangente de un ángulo (teta) es el cociente entre el cateto opuesto y el cateto adyacente.
- 📏 La secante es la función trigonométrica opuesta al coseno, y se define como la relación entre la hipotenusa y el cateto adyacente.
- 📏 La cotangente es la función opuesta a la tangente, y se calcula como la relación entre la hipotenusa y el cateto opuesto.
- 📏 Las funciones trigonométricas se pueden expresar tanto en forma de fracciones como en decimales.
- 📏 Al identificar correctamente el cateto opuesto, el cateto adyacente y la hipotenusa, se pueden calcular las razones trigonométricas de un ángulo dado.
- 📏 En un triángulo rectángulo, la hipotenusa es el lado más largo y está opuesto al ángulo recto.
- 📏 Las unidades de medida, como metros o centímetros, se eliminan al calcular las razones trigonométricas, ya que se trata de relaciones entre longitudes.
- 📏 El entendimiento de las relaciones opuestas entre las funciones trigonométricas (como la tangente y la cotangente) ayuda a simplificar los cálculos y comprensión del concepto.
Q & A
¿Qué es lo primero que debemos conocer para encontrar las razones trigonométricas de un ángulo?
-Lo primero que debemos conocer son las fórmulas de las razones trigonométricas, como el seno, el coseno y la tangente.
¿Cómo se define el cateto opuesto y el cateto adyacente en un triángulo rectángulo?
-El cateto opuesto es el lado que está opuesto al ángulo en cuestión, mientras que el cateto adyacente es el lado que está pegado o adyacente al ángulo.
¿Cuál es la fórmula para calcular el seno de un ángulo en un triángulo rectángulo?
-La fórmula para calcular el seno de un ángulo es cateto opuesto sobre hipotenusa.
¿Cómo se calcula el coseno de un ángulo en trigonometría?
-El coseno de un ángulo se calcula como cateto adyacente sobre hipotenusa.
¿Qué es la tangente en trigonometría y cómo se calcula?
-La tangente es la relación entre el cateto opuesto y el cateto adyacente de un ángulo en un triángulo rectángulo, es decir, cateto opuesto sobre cateto adyacente.
¿Cómo se relacionan las razones trigonométricas opuestas, como la tangente y la cotangente?
-Las razones trigonométricas opuestas son inversas entre sí. Por ejemplo, si la tangente es cateto opuesto sobre cateto adyacente, la cotangente sería cateto adyacente sobre cateto opuesto.
¿Por qué se eliminan las unidades de medida al calcular las razones trigonométricas?
-Las unidades de medida, como metros o centímetros, se eliminan porque las razones trigonométricas son relaciones de proporciones que no dependen de la magnitud de los lados sino de su relación entre sí.
¿Cómo se calcula la secante de un ángulo?
-La secante de un ángulo se calcula como la hipotenusa sobre el cateto adyacente.
¿Cómo se verifica que la secante es la razón trigonométrica opuesta al coseno?
-Se verifica al observar que si el coseno es cateto adyacente sobre hipotenusa, la secante, que es la razón opuesta, sería hipotenusa sobre cateto adyacente.
¿Por qué es importante ordenar las razones trigonométricas de cierta manera al calcularlas?
-Es importante ordenarlas para no confundirse y poder aplicar eficientemente las relaciones entre ellas, como la relación de opuestos que existe entre la tangente y la cotangente, o entre la secante y el coseno.
¿Cómo se pueden expresar las razones trigonométricas,除了分数形式,还可以怎样表示?
-Además de expresarse en forma de fracción, las razones trigonométricas también se pueden escribir en forma decimal, realizando la división numérica correspondiente.
¿Cuál es el propósito del ejercicio que se presenta al final del script?
-El ejercicio al final del script tiene como propósito permitir a los estudiantes practicar y consolidar los conceptos aprendidos sobre las razones trigonométricas en diferentes situaciones.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Introducción a Trigonometría
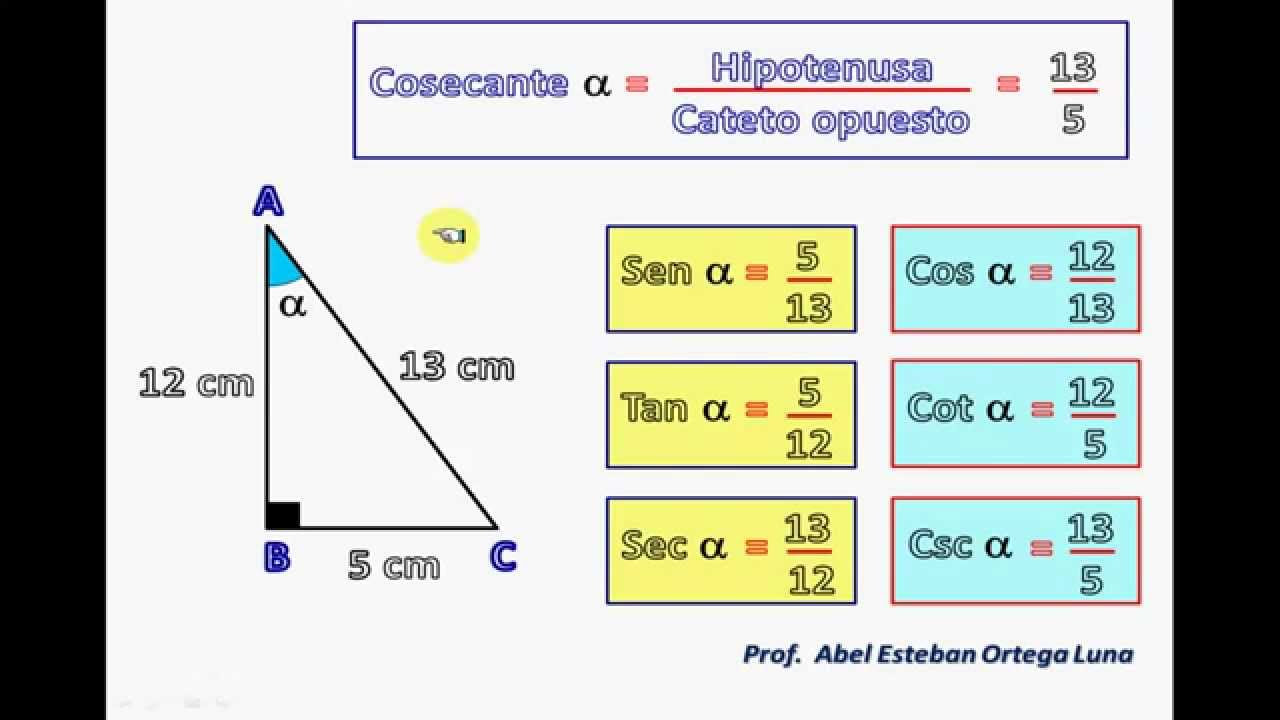
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Usar relaciones en triángulos rectángulos para aproximar la medida de un ángulo

Ecuaciones Trigonométricas. Parte 1 (Introduccion y Ejercicios)

Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1

Seno, coseno y tangente de 30° 45° 60° | Sin calculadora
5.0 / 5 (0 votes)
