Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1
Summary
TLDREn este video, se explica cómo resolver un triángulo rectángulo utilizando razones trigonométricas. Se comienza identificando los ángulos y los lados del triángulo, luego se encuentra el tercer ángulo mediante la propiedad de que la suma de los ángulos internos de un triángulo es 180 grados. A continuación, se calculan los lados utilizando las funciones trigonométricas, específicamente el seno y la tangente. El video también ofrece ejemplos de cómo aplicar el teorema de Pitágoras y las razones trigonométricas para hallar la hipotenusa y el cateto restante. Finalmente, se deja un ejercicio para que los espectadores practiquen.
Takeaways
- 😀 El triángulo que se va a resolver es un triángulo rectángulo con un ángulo de 90 grados y otro de 56 grados.
- 😀 Para resolver un triángulo rectángulo, es necesario conocer los tres ángulos y los tres lados del triángulo.
- 😀 Se puede calcular el tercer ángulo de un triángulo rectángulo restando los otros dos ángulos de 180 grados.
- 😀 Los lados del triángulo rectángulo se nombran como cateto opuesto, cateto adyacente e hipotenusa.
- 😀 La hipotenusa se puede calcular usando la función seno, que involucra el cateto opuesto y la hipotenusa.
- 😀 Para calcular la hipotenusa, se usa la fórmula: seno del ángulo = cateto opuesto / hipotenusa.
- 😀 El valor de la hipotenusa en el ejemplo es 12,06 metros, calculado usando la función seno de 56 grados.
- 😀 Para encontrar el cateto adyacente, se puede usar la función tangente, que relaciona el cateto opuesto y el cateto adyacente.
- 😀 La fórmula para calcular el cateto adyacente es: tangente del ángulo = cateto opuesto / cateto adyacente.
- 😀 El cateto adyacente se encuentra realizando la operación 10 metros dividido entre la tangente de 56 grados, resultando en 6,75 metros.
- 😀 Finalmente, se repasan los tres ángulos y los tres lados del triángulo rectángulo, concluyendo que se ha resuelto correctamente el problema.
Q & A
¿Qué significa resolver un triángulo rectángulo?
-Resolver un triángulo rectángulo significa encontrar todos los datos que faltan, como los ángulos y los lados del triángulo, utilizando las razones trigonométricas o el teorema de Pitágoras.
¿Qué debe sumarse en los triángulos rectángulos?
-Los ángulos internos de cualquier triángulo deben sumar 180 grados. En un triángulo rectángulo, uno de esos ángulos es de 90 grados.
¿Cómo se calcula el tercer ángulo en un triángulo rectángulo?
-El tercer ángulo se calcula restando los dos ángulos conocidos de 180 grados. En este caso, si tenemos 90 y 56 grados, la resta da 34 grados.
¿Cómo se nombran los lados de un triángulo rectángulo?
-En un triángulo rectángulo, los lados se nombran como cateto opuesto, cateto adyacente e hipotenusa. La hipotenusa es el lado opuesto al ángulo recto.
¿Qué fórmula trigonométrica se utiliza para encontrar la hipotenusa?
-Para encontrar la hipotenusa, se usa la fórmula del seno: seno del ángulo = cateto opuesto / hipotenusa.
¿Cómo se utiliza el seno para encontrar la hipotenusa?
-Se sustituye en la fórmula: seno del ángulo = cateto opuesto / hipotenusa. Luego, despejando la hipotenusa, se realiza la operación: hipotenusa = cateto opuesto / seno del ángulo.
¿Qué operación se realiza para encontrar la hipotenusa si el cateto opuesto mide 10 metros y el ángulo es de 56 grados?
-La operación sería: hipotenusa = 10 metros / seno de 56 grados. Esto da un resultado de 12.06 metros.
¿Cuál es la fórmula trigonométrica adecuada para encontrar un cateto cuando se conocen el cateto opuesto y el cateto adyacente?
-La fórmula adecuada es la tangente: tangente del ángulo = cateto opuesto / cateto adyacente.
¿Cómo se encuentra el cateto adyacente utilizando la tangente?
-Se usa la fórmula tangente del ángulo = cateto opuesto / cateto adyacente. Despejando el cateto adyacente, se realiza la operación: cateto adyacente = cateto opuesto / tangente del ángulo.
¿Qué se recomienda hacer cuando no se conocen todos los datos de un triángulo rectángulo?
-Se recomienda usar las funciones trigonométricas adecuadas, como el seno, coseno o tangente, para encontrar los valores desconocidos, o aplicar el teorema de Pitágoras si se conocen dos lados.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
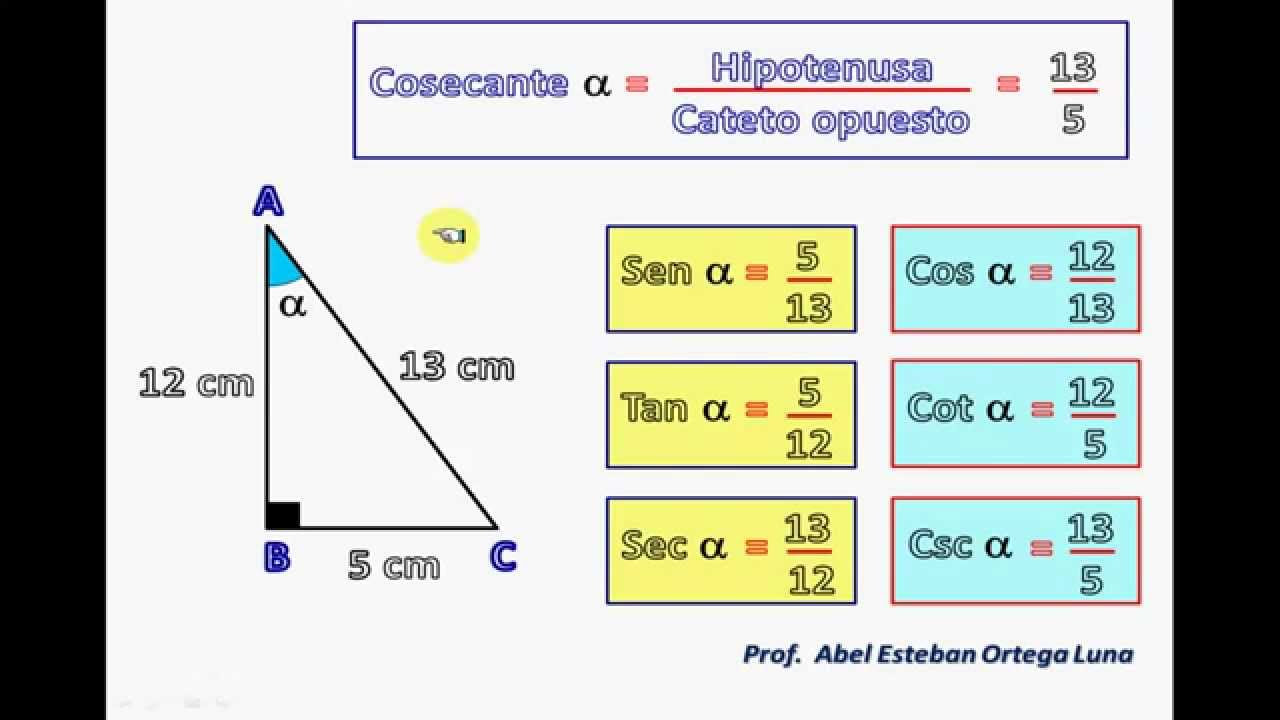
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Como calcular los lados de un triángulo rectángulo conociendo un lado y un angulo

Razones trigonométricas de un ángulo | Ejemplo 1

Razones Trigonométricas

RESOLUCIÓN de TRIÁNGULOS RECTÁNGULOS |ACADEMIA INTERNET nos desafía 😱

Como saber cuando usar el seno, coseno y tangente
5.0 / 5 (0 votes)
