Seno, coseno y tangente de 30° 45° 60° | Sin calculadora
Summary
TLDREn este video, se exploran las funciones trigonométricas de ángulos especiales: 30°, 45° y 60°. Utilizando un triángulo equilátero para 30° y 60°, se calculan el seno, coseno y tangente de ambos ángulos, demostrando sus relaciones y propiedades. Luego, se introduce un triángulo isósceles para el ángulo de 45°, derivando las funciones trigonométricas correspondientes. El instructor anima a los espectadores a practicar y a consultar otros recursos para mejorar su comprensión de las razones trigonométricas, mientras invita a suscribirse y participar en su canal.
Takeaways
- 😀 El curso se centra en las funciones trigonométricas para ángulos especiales: 30°, 45° y 60°.
- 📐 Se utiliza un triángulo equilátero para calcular las funciones trigonométricas del ángulo de 60°.
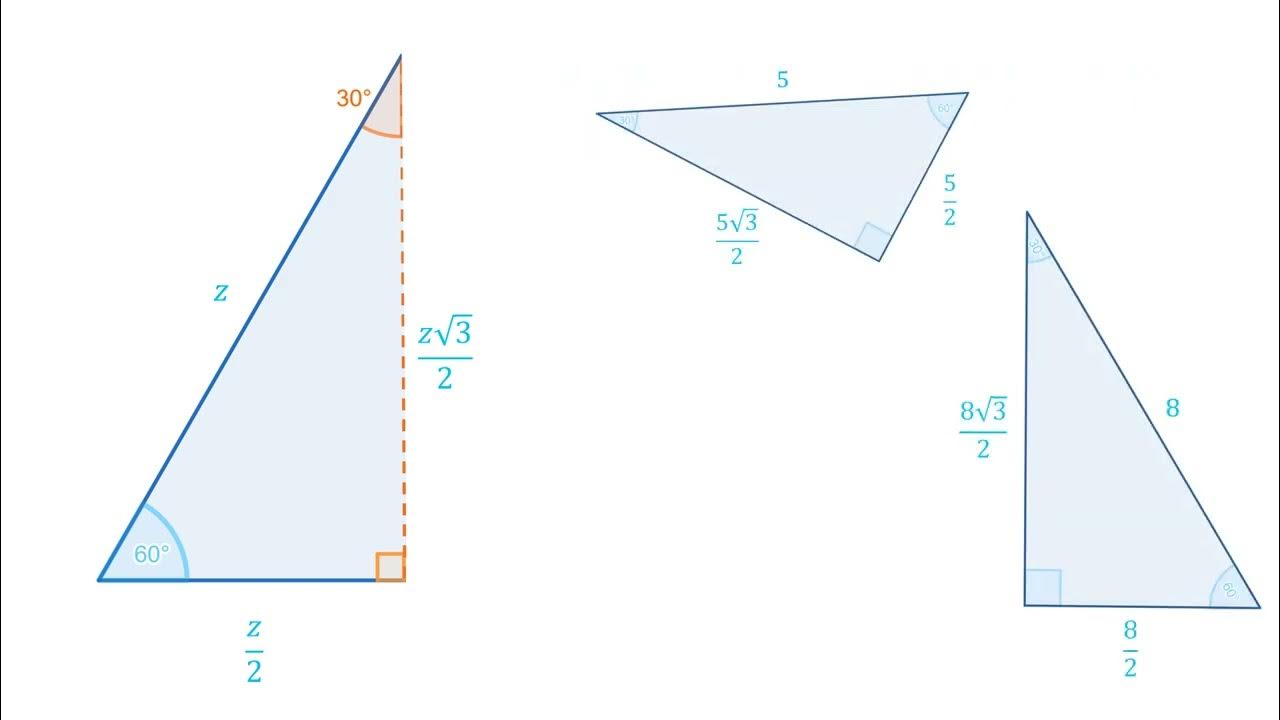
- 🔺 En un triángulo 30°-60°-90°, los lados tienen proporciones fijas: hipotenusa = 2, cateto opuesto = 1, cateto adyacente = √3.
- 📊 Para el ángulo de 30°: seno = 1/2, coseno = √3/2, tangente = 1/√3.
- 📏 El ángulo de 60° tiene las funciones trigonométricas inversas: seno = √3/2, coseno = 1/2, tangente = √3.
- ⚖️ En el triángulo isósceles de 45°, ambos catetos son iguales, facilitando los cálculos de las funciones.
- ➕ Para el ángulo de 45°: seno = 1/√2, coseno = 1/√2, tangente = 1.
- 🔄 Las funciones inversas incluyen cosecante, secante y cotangente, derivadas de las funciones originales.
- 🔍 El teorema de Pitágoras es fundamental para determinar las longitudes de los lados en los triángulos utilizados.
- 📚 Se sugiere a los estudiantes practicar y revisar el contenido anterior para reforzar su comprensión.
Q & A
¿Cuáles son las funciones trigonométricas que se encuentran para el ángulo de 30 grados?
-Las funciones trigonométricas para el ángulo de 30 grados son: seno de 30 grados es 1/2, coseno de 30 grados es raíz de 3/2, y tangente de 30 grados es 1/raíz de 3.
¿Por qué se utiliza un triángulo equilátero en el primer ejercicio?
-Se utiliza un triángulo equilátero porque todos sus lados y ángulos son iguales, lo que facilita el cálculo de las funciones trigonométricas para los ángulos de 30 y 60 grados.
¿Cómo se determina el valor de la altura de un triángulo equilátero?
-La altura de un triángulo equilátero divide el lado de abajo en dos partes iguales y se puede calcular usando el teorema de Pitágoras.
¿Qué relación existe entre los ángulos internos de un triángulo equilátero?
-Todos los ángulos internos de un triángulo equilátero miden 60 grados, y por lo tanto, la suma de los ángulos internos es 180 grados.
¿Cuáles son las funciones trigonométricas del ángulo de 60 grados?
-Las funciones trigonométricas para el ángulo de 60 grados son: seno de 60 grados es raíz de 3/2, coseno de 60 grados es 1/2, y tangente de 60 grados es raíz de 3.
¿Qué tipo de triángulo se utiliza para calcular las funciones trigonométricas del ángulo de 45 grados?
-Se utiliza un triángulo isósceles, donde dos lados son iguales y el ángulo recto forma dos ángulos de 45 grados.
¿Cómo se calcula la hipotenusa en un triángulo isósceles de 45 grados?
-Se calcula usando el teorema de Pitágoras, donde el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Qué valores se obtienen para las funciones trigonométricas del ángulo de 45 grados?
-Las funciones trigonométricas para el ángulo de 45 grados son: seno de 45 grados es 1/raíz de 2, coseno de 45 grados es 1/raíz de 2, y tangente de 45 grados es 1.
¿Cuál es la importancia de las funciones trigonométricas inversas?
-Las funciones trigonométricas inversas, como la cosecante, secante y cotangente, son importantes porque permiten calcular los lados de un triángulo cuando se conocen las funciones trigonométricas básicas.
¿Qué se recomienda hacer si los conceptos no quedan claros?
-Se recomienda revisar los videos anteriores del curso para una comprensión más detallada de las funciones trigonométricas y el teorema de Pitágoras.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Círculo trigonométrico (PRIMERA PARTE)

Identidades Trigonométricas | Identidad Pitagórica | Identidades de Cofunciones |

Identidades trigonométricas de resta de ángulos | Seno y Coseno de 15° sin calculadora

Identidades trigonométricas de suma de ángulos | Seno y Coseno de 75° sin calculadora
Razones Trigonométricas en Triángulos Especiales

Cómo trazar Ángulos con Escuadra y Cartabón: 15º, 75º, 45º, 60º, 30º, 90º, 165º, 105º, 135º y más.
5.0 / 5 (0 votes)
