How to make Forecasting! | Quantitative Forecasting with Least Squares Method | Quickly & easily
Summary
TLDRThis video introduces the Quantitative Forecasting with the Least Squares Method, a regression analysis technique used to predict future demand based on historical data. By explaining key concepts such as the y-axis intercept, slope, and the necessary calculations for time periods and values, viewers learn how to formulate the least squares equation. The example forecasts demand for 2024, illustrating the process step-by-step. This engaging tutorial is perfect for anyone looking to enhance their forecasting skills using the Least Squares Method.
Takeaways
- 📊 Forecasting uses historical data to make informed predictions about future events.
- 🗓️ The demand data from 2017 to 2023 serves as the basis for predicting demand in 2024.
- 📈 The least squares method is a regression analysis technique used to identify trading opportunities.
- 🔢 The formula for the least squares method involves determining the intercept (a) and slope (b) of the regression line.
- 📏 The known values of the independent variable (x) and dependent variable (y) are essential for the calculations.
- 📊 The averages of the x-values (x̅) and y-values (y̅) play a crucial role in determining the regression equation.
- 🧮 The least squares equation is derived from the values of a and b to project future demand.
- 🔍 To forecast demand in 2024, the year is represented as x = 8 in the equation.
- 📅 The projected demand for 2024 is calculated to be 141.02 using the least squares equation.
- 🎉 The video encourages viewers to learn and subscribe for more insights on forecasting techniques.
Q & A
What is the purpose of forecasting in business?
-Forecasting is a technique that uses historical data to make informed decisions about future events or conditions.
What is the least squares method?
-The least squares method is a form of regression analysis used to identify trading opportunities and market trends.
What are the main components of the least squares equation?
-The main components include the y-axis intercept (a), the slope of the regression line (b), known values of the independent variable (x), and known values of the dependent variable (y).
How do you calculate the y-intercept (a) in the least squares method?
-The y-intercept (a) is calculated using the formula: a = 𝑦̅ - b𝑥̅, where 𝑦̅ is the average of the y-values and 𝑥̅ is the average of the x-values.
What is the formula for the least squares equation?
-The least squares equation is expressed as y = a + bx, where 'a' is the y-intercept and 'b' is the slope.
How is the demand for 2024 projected in this method?
-To project the demand for 2024, the year is denoted as x = 8, and the demand is calculated using the least squares equation.
What were the calculated values for the slope (b) and y-intercept (a) in this example?
-In this example, the y-intercept (a) is 56.70 and the slope (b) is 10.54.
What is the final demand projection for the year 2024?
-The projected demand for 2024 is 141.02.
What is the significance of the summation sign (∑) in the least squares method?
-The summation sign (∑) represents the sum of the values, which is crucial for calculating averages and other components in the least squares calculations.
What key information does the average of x-values (x̅) and y-values (y̅) provide?
-The average of the x-values (x̅) and y-values (y̅) are used to determine the central tendency of the data, which is essential for calculating the slope and intercept in the least squares method.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

How to Select the Correct Predictive Modeling Technique | Machine Learning Training | Edureka

Introduction to Time Series Forecasting | SCMT 3623
Regresion Lineal
PRONOSTICOS DE VENTAS (Modelo Regresión Lineal)

Penggunaan Metode Least Square Dalam Ramalan Penjualan
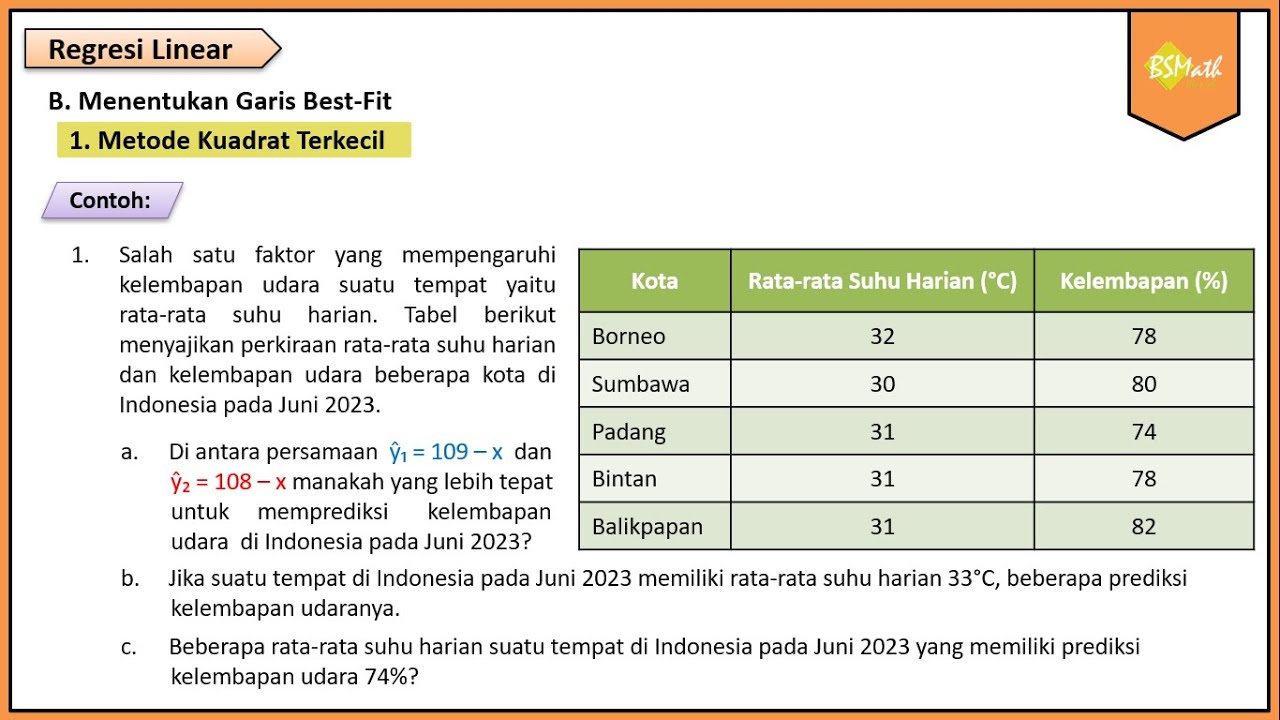
Contoh Soal dan Pembahasan Metode Kuadrat Terkecil - Matematika Wajib Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)