Resolving Vectors
Summary
TLDRThis lesson on resolving vectors, part of AQA A Level Physics, explores how to break down vector quantities into their horizontal and vertical components. It emphasizes the independence of these components and their role in analyzing motion. Through trigonometric relationships, students learn to calculate components from resultant vectors using sine and cosine functions. Practical examples, such as a trolley on a slope, illustrate the application of these concepts in real-world scenarios. The lesson concludes by reinforcing the importance of vector resolution in understanding mechanics and solving physics problems effectively.
Takeaways
- 😀 Vectors are quantities that have both magnitude and direction, unlike scalars which only have magnitude.
- 🧮 A resultant vector can be resolved into two perpendicular components: horizontal (Fₓ) and vertical (Fᵧ).
- 🔗 The process of resolving vectors means splitting them into their components, which allows for easier analysis of motion.
- 📐 The Pythagorean theorem can be used to relate a resultant vector to its components: F² = Fᵧ² + Fₓ².
- 📏 For any angle θ, the horizontal component is calculated as Fₓ = F * cos(θ), and the vertical component as Fᵧ = F * sin(θ).
- 🌍 Real-world applications include analyzing forces acting on objects, such as a trolley on a slope.
- 🔍 The angle used in calculations must be the angle produced by the vectors, not just a reference direction.
- 📊 When resolving vectors, remember that the components do not add directly due to their directions; instead, they create a resultant vector.
- 📐 The scale diagram method can also be used to resolve vectors by creating right-angle triangles and measuring the components.
- 🧑🎓 Understanding vector resolution is crucial for solving physics problems related to forces and motion, especially in inclined plane scenarios.
Q & A
What are vector quantities?
-Vector quantities are physical quantities that have both magnitude and direction, such as force, velocity, and displacement.
How can resultant vectors be resolved?
-Resultant vectors can be resolved into their horizontal and vertical components using trigonometric functions, specifically sine and cosine.
What does the term 'resolve' mean in the context of vectors?
-In the context of vectors, 'resolve' means to split a resultant vector into its perpendicular components.
What is the Pythagorean theorem's role in vector resolution?
-The Pythagorean theorem is used to calculate the magnitude of the resultant vector when its components are known, expressed as F² = Fy² + Fx².
What are the equations used to find horizontal and vertical components?
-The horizontal component (Fx) is found using Fx = F cos(Theta), and the vertical component (Fy) is found using Fy = F sin(Theta).
How do you determine the components of a vector with a magnitude of 6 m/s at 60 degrees from the horizontal?
-The horizontal component is 3 m/s (6 cos(60)), and the vertical component is 5.2 m/s (6 sin(60)).
What is the significance of perpendicular components in vector resolution?
-Perpendicular components are independent of each other, allowing for separate analysis of their effects on motion.
What is a scale diagram method for resolving vectors?
-A scale diagram method involves drawing a right triangle representing the resultant vector and measuring the lengths of its components to determine their values.
How does the weight of an object on a slope affect its motion?
-The weight of an object has a component acting down the slope, which determines its acceleration down the slope, while the normal force acts perpendicular to the slope and does not contribute to acceleration.
Why is it important to resolve vectors in the most logical directions?
-Resolving vectors in logical directions simplifies the analysis, especially in complex scenarios such as inclined planes, allowing for clearer understanding and calculation of motion.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Scalars and Vectors

Vectors and 2D Motion: Crash Course Physics #4
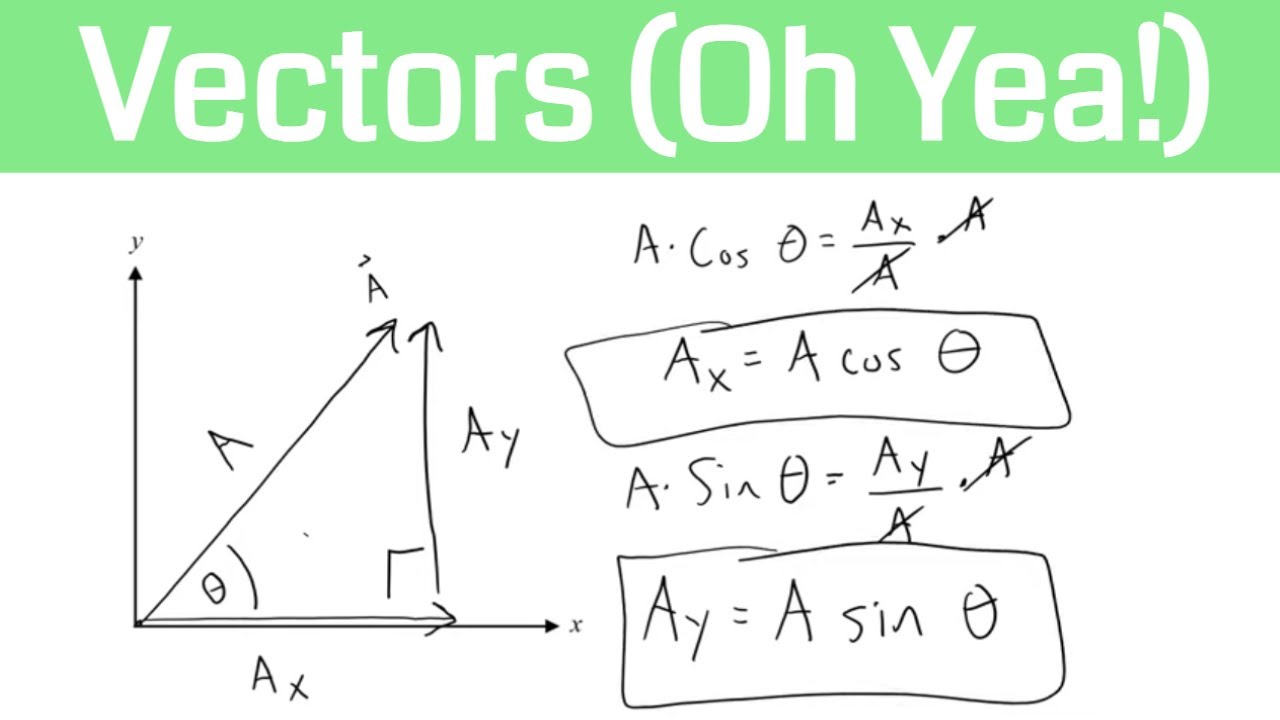
How to Find X and Y Components of Vectors

Vektor Matematika Kelas 10 • Part 1: Definisi Vektor & Cara Menyatakan Vektor

VEKTOR: PENGERTIAN DAN PENJUMLAHAN - MATERI FISIKA KELAS 10 | Edcent.id

BESARAN BERDASARKAN ARAHNYA | Vektor #1 - Fisika Kelas 10
5.0 / 5 (0 votes)