How to Find X and Y Components of Vectors
Summary
TLDRThis video tutorial explains how to resolve a vector into its horizontal (x) and vertical (y) components. It begins by illustrating how vectors form right triangles, with the vector's magnitude as the hypotenuse. Using trigonometric functions, cosine is applied for the x-component (adjacent) and sine for the y-component (opposite). The tutorial walks through several examples, calculating the x and y components for vectors at different angles and magnitudes, and clarifies how to properly handle angles relative to the unit circle. The lesson concludes by emphasizing the importance of resolving vectors in physics and math.
Takeaways
- 📐 Vectors have components that are essentially their x (horizontal) and y (vertical) values, with the tail at the origin and the head labeled with the vector.
- 🔼 The x and y components form a right triangle with the vector, allowing the use of trigonometric functions like sine, cosine, and tangent to resolve them.
- 🔵 The x component (Ax) is adjacent to the angle theta and is calculated as Ax = A * cos(theta).
- 🔺 The y component (Ay) is opposite to the angle theta and is calculated as Ay = A * sin(theta).
- 🧮 For vector A with a magnitude of 4.1 and an angle of 14 degrees, Ax is approximately 4, and Ay is approximately 1, using cosine and sine functions.
- ↔️ When a vector points left (e.g., vector B), the x component becomes negative, but the same sine and cosine rules apply.
- 🔄 Using the unit circle helps ensure that the sine and cosine of the angle always yield the correct components (positive or negative).
- 🧊 Non-unit circle angles require extra care, as sine and cosine might not automatically reflect the direction (positive/negative) of components.
- 📊 Resolving vectors into their x and y components helps identify their direction and magnitude using basic trigonometry.
- 🚩 The overall goal is to decompose vectors into their components, facilitating problem-solving with right triangles and trigonometric relationships.
Q & A
What are the components of a vector, and how are they represented?
-The components of a vector are its horizontal (x) and vertical (y) parts. These components are like the x and y coordinates of the vector. The horizontal component is labeled as Ax, and the vertical component is labeled as Ay.
How do you create a right triangle with a vector's components?
-You can create a right triangle by moving the x or y component over. The vector serves as the hypotenuse, with the x and y components being the two legs of the triangle. The angle between the vector and the x-axis forms the angle used for calculations.
How can you calculate the x-component (Ax) of a vector?
-The x-component (Ax) of a vector is calculated using the formula: Ax = A * cos(θ), where A is the magnitude of the vector and θ is the angle between the vector and the x-axis.
How do you calculate the y-component (Ay) of a vector?
-The y-component (Ay) of a vector is calculated using the formula: Ay = A * sin(θ), where A is the magnitude of the vector and θ is the angle between the vector and the x-axis.
What is the significance of the signs of the vector components?
-The sign of the x-component indicates direction along the x-axis (positive means right, negative means left), and the sign of the y-component indicates direction along the y-axis (positive means up, negative means down).
Why do we use cosine for the x-component and sine for the y-component?
-Cosine is used for the x-component because the x-component is adjacent to the angle in the right triangle, and sine is used for the y-component because the y-component is opposite to the angle.
How does using a 'unit circle angle' simplify vector component calculations?
-Using the unit circle angle simplifies calculations because cosine always gives the correct x-component, and sine always gives the correct y-component. The signs are automatically handled based on the angle's quadrant.
What happens if you don't use the unit circle angle?
-If you don't use the unit circle angle, you will have to manually adjust the signs of the components based on their direction. For example, a leftward x-component or downward y-component would need to be negative.
How do you calculate vector components for non-standard angles like 26.6 degrees?
-For non-standard angles like 26.6 degrees, you can either add 90 degrees to find the unit circle angle or calculate the components using sine and cosine directly and manually adjust the signs based on the vector's direction.
What is the process of resolving a vector into its components?
-Resolving a vector into its components involves breaking it into its horizontal (x) and vertical (y) parts using trigonometric functions, such as cosine for the x-component and sine for the y-component. The process ensures you can work with simpler components rather than the whole vector.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Resolve each force acting on the post into its x and y components.

Movimiento parabólico - Ecuaciones
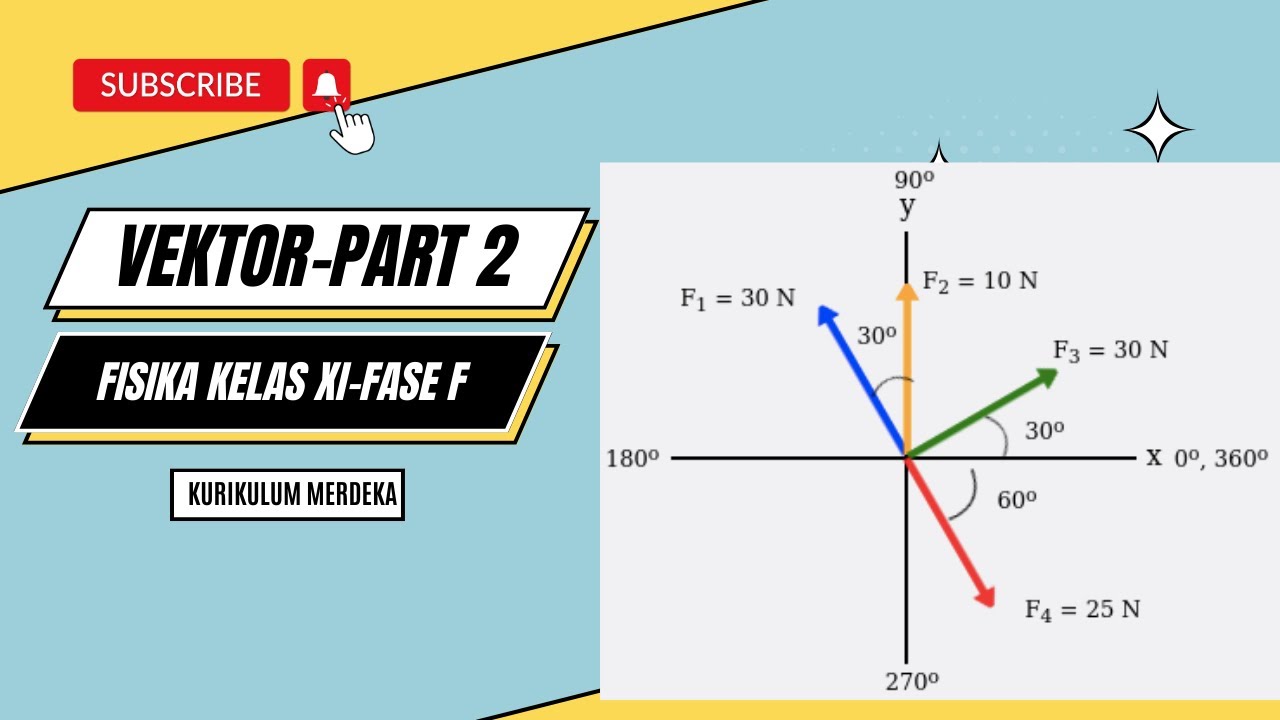
FISIKA VEKTOR KELAS XI [FASE F] PART 2 - KURIKULUM MERDEKA

Vektor Matematika Kelas 10 • Part 1: Definisi Vektor & Cara Menyatakan Vektor

What Are Vector Components?

Resolution of Forces: Horizontal & Vertical Components + Resultant Force Explained!
5.0 / 5 (0 votes)