Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy
Summary
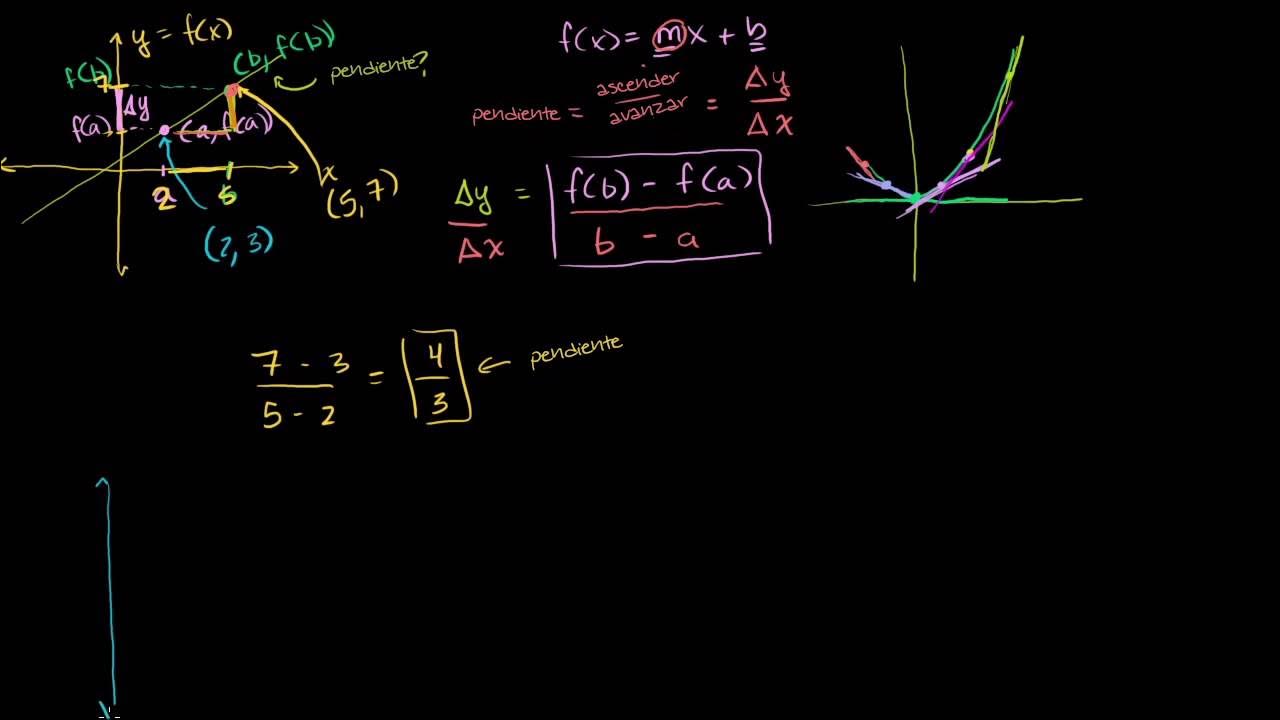
TLDRThis video script explains the concept of finding the slope of a curve at a specific point by using the slope of a secant line between two points. As the distance between the points decreases, the secant line's slope approaches the slope of the tangent line. The derivative of a function, represented as f'(x), is introduced as the slope of the tangent line. The example uses the function y = x^2 to find the slope at x = 3, demonstrating the process of taking the limit as the secant line approaches the tangent line, resulting in a slope of 6.
Takeaways
- 📐 The concept of slope of a curve at a specific point is introduced.
- 🔍 The slope of a secant line is calculated by taking two points on the curve, with one point not too far from the other.
- 📈 The change in y (Δy) divided by the change in x (Δx) gives the slope of the secant line.
- 🎯 The slope of the tangent line at a specific point is approached as the secant line gets closer to that point.
- 🧭 The derivative of a function at a point is defined as the slope of the tangent line at that point.
- 📉 The process of finding the slope at a specific point is demonstrated using the curve y = x^2 at x = 3.
- 🔢 The notation 'delta x' (Δx) is used to represent a small change in x, which is a common notation in calculus.
- 📋 The slope of the secant line simplifies to 6 + Δx when considering the curve y = x^2.
- 📉 As Δx approaches 0, the slope of the secant line approaches the slope of the tangent line, which is the derivative of the function at that point.
- 🔄 The limit as Δx approaches 0 of the slope of the secant line gives the slope of the tangent line, which is 6 at x = 3 for y = x^2.
Q & A
What is the main concept discussed in the video script?
-The main concept discussed in the video script is the calculation of the slope of a curve at a specific point, which is the derivative of a function at that point.
How is the slope of a curve at a point determined?
-The slope of a curve at a point is determined by finding the slope of the secant line between that point and another point close to it, and then taking the limit as the second point approaches the first point.
What is the secant line in the context of this video?
-The secant line in this video is a line that passes through two points on the curve, and its slope is calculated using the change in y divided by the change in x between these two points.
How is the slope of the secant line related to the slope of the tangent line?
-The slope of the secant line approaches the slope of the tangent line as the second point on the curve gets closer to the first point.
What does the derivative of a function represent?
-The derivative of a function represents the slope of the tangent line to the curve of the function at a specific point.
What is the function used as an example in the video script?
-The function used as an example in the video script is f(x) = x^2.
At which point on the curve does the video script focus on finding the slope?
-The video script focuses on finding the slope of the curve at the point where x equals 3.
What is the significance of the notation change from 'h' to 'delta x'?
-The notation change from 'h' to 'delta x' is to expose viewers to different notations used in various books and to emphasize that the concept remains the same regardless of the symbol used.
What is the formula for the slope of the secant line in terms of delta x?
-The formula for the slope of the secant line in terms of delta x is (f(x + delta x) - f(x)) / ((x + delta x) - x), which simplifies to (9 + 6 delta x + delta x^2 - 9) / delta x.
How does the slope of the secant line simplify when delta x approaches 0?
-When delta x approaches 0, the slope of the secant line simplifies to 6, which is the derivative of the function f(x) = x^2 at x = 3.
What is the limit process described in the video script?
-The limit process described in the video script is taking the limit of the slope of the secant line as delta x approaches 0, which results in the slope of the tangent line.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)