KALKULUS | TURUNAN | APA ITU TURUNAN?

Summary

This video focuses on explaining the concept of derivatives in calculus, starting from the fundamental idea of secant lines and progressing to tangents. The script introduces the concept of calculating the slope of a secant line using the limit as the two points approach each other. The derivative is then defined as the slope of the tangent line at a point. The video includes examples showing how to compute derivatives for quadratic functions, explaining the process step by step. It also covers finding the derivative at a specific point, providing a comprehensive understanding of derivatives and their practical applications.

Takeaways

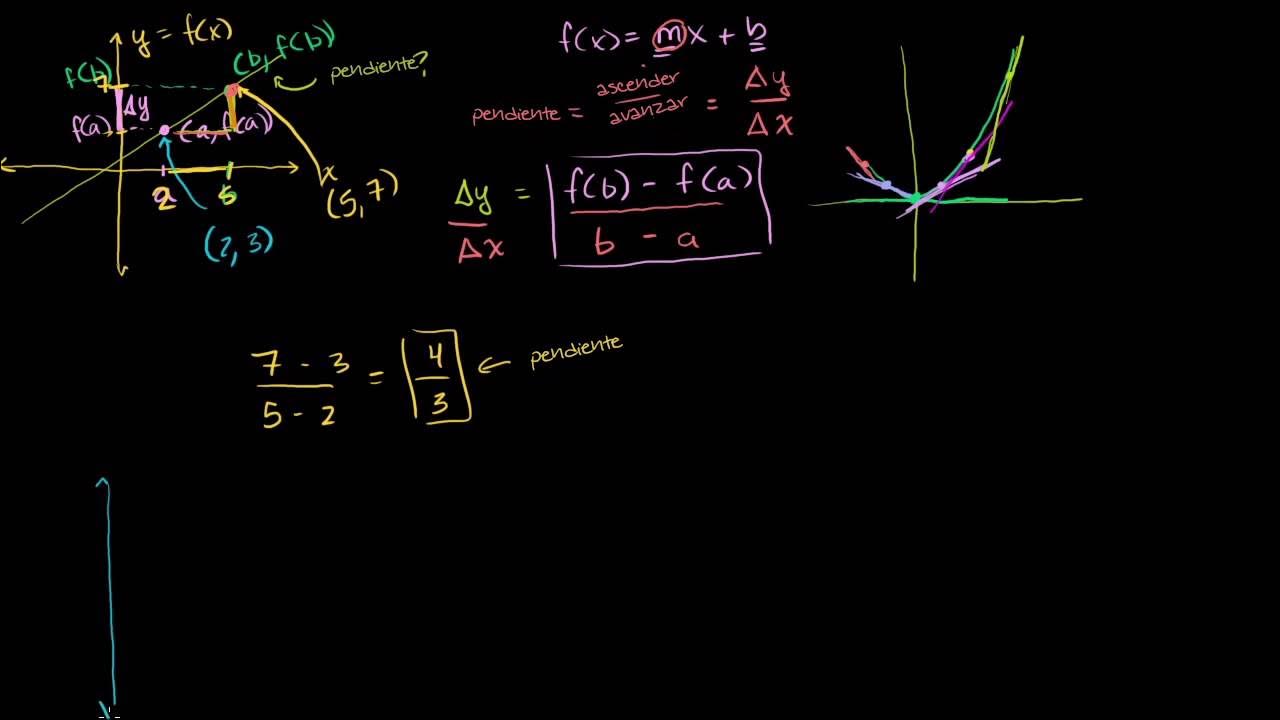
• 😀 The concept of derivatives in calculus originates from the slope of a secant line between two points on a curve.
• 😀 A secant line intersects the curve at two points, and its slope can be calculated by dividing the vertical difference (y-values) by the horizontal difference (x-values).
• 😀 As the second point (Q) moves closer to the first point (P), the secant line becomes a tangent line, touching the curve at only one point.
• 😀 The derivative (denoted as f'(x)) of a function is the limit of the slope of the secant line as the second point approaches the first point, or as the horizontal difference (h) approaches zero.
• 😀 The slope of the tangent line at a given point on the curve represents the derivative of the function at that point.
• 😀 The formal definition of a derivative is the limit of the difference quotient: f'(x) = limit as h approaches 0 of [f(x+h) - f(x)] / h.
• 😀 The first example demonstrates how to calculate the derivative of a quadratic function (2x²), yielding a result of 4x.
• 😀 In the second example, the derivative of the function (x² - 2x) is computed, resulting in 2x - 2.
• 😀 For specific values of x, the derivative is evaluated at a given point. For example, for x = 2, the derivative of the function f(x) = x² is 4.
• 😀 In further examples, the script shows the process of calculating derivatives and substituting values to find the slope of the tangent at specific points on the curve, including negative values and fractional results.

Q & A

What is the concept of the derivative in calculus as explained in the video?

The derivative in calculus is explained as the slope of the tangent line to a function's curve at a specific point. It is derived from the concept of the secant line (or 'chord') that connects two points on the curve. As the two points get closer, the secant line becomes the tangent line, and its slope at that point is the derivative.

What is the process for calculating the slope of the secant line in the given explanation?

The slope of the secant line is calculated by taking the difference in the function values at two points, (f(x+h) - f(x)), and dividing it by the difference in their x-values, which is h. This gives the formula (f(x+h) - f(x)) / h for the slope of the secant line.

How does the secant line become the tangent line?

As the point Q (on the secant line) moves closer to point P on the curve, the secant line approaches the tangent line. When point Q coincides with point P, the secant line becomes the tangent line, which touches the curve at exactly one point and represents the instantaneous rate of change at that point.

What happens to the slope of the secant line as the distance h approaches zero?

As h approaches zero, the slope of the secant line approaches the slope of the tangent line. This is the essence of the derivative in calculus, representing the instantaneous rate of change of the function at a specific point.

What is the formal definition of the derivative as presented in the video?

The derivative of a function at a point x = a is defined as the limit of the difference quotient (f(a+h) - f(a)) / h as h approaches zero. This limit gives the slope of the tangent line at the point x = a.

What is the first example of calculating a derivative in the video?

The first example involves finding the derivative of the function f(x) = 2x². Using the definition of the derivative, the limit is computed, and the derivative is found to be f'(x) = 4x.

How is the derivative of the function f(x) = x² - 2x calculated?

For f(x) = x² - 2x, the derivative is calculated by applying the difference quotient. After simplifying the expression and taking the limit as h approaches zero, the derivative is found to be f'(x) = 2x - 2.

What is the method for calculating the derivative at a specific point, such as x = 2?

To calculate the derivative at x = 2, the difference quotient is used with the specific value of x. After substituting x = 2 into the function and performing the necessary algebra, the result is f'(2) = 4, indicating the slope of the tangent line at x = 2.

How is the derivative of a constant function, such as f(x) = 1/3, calculated?

For a constant function like f(x) = 1/3, the derivative is zero. This is because the function has no change in its value at any point, so the slope of the tangent line is zero.

What is the process for calculating the derivative of a function at a specific point, like f'(3) for the function f(x) = -x² + 6x + 2?

To calculate the derivative at x = 3 for f(x) = -x² + 6x + 2, the difference quotient is used. After simplifying the expression, the derivative at x = 3 is found to be f'(3) = -4, indicating the slope of the tangent line at that point.